叠加定理
在线性电路中,任一支路的电流(或电压)可以看成是电路中每一个独立电源单独作用于电路时,在该支路产生的电流(或电压)的代数和。
结点电压和支路电流均为各电源的一次函数,均可看成各独立电源单独作用时,产生的响应之叠加。
使用叠加定理注意事项:
- 叠加定理只适用于线性电路。
- 一个电源作用,其余电源为零。电压源为零——短路,电流源为零——开路。
- 功率不能叠加。
- u ,i 叠加时要注意各分量的参考方向。
- 含受控源(线性)电路亦可用叠加,但受控源应始终保留。
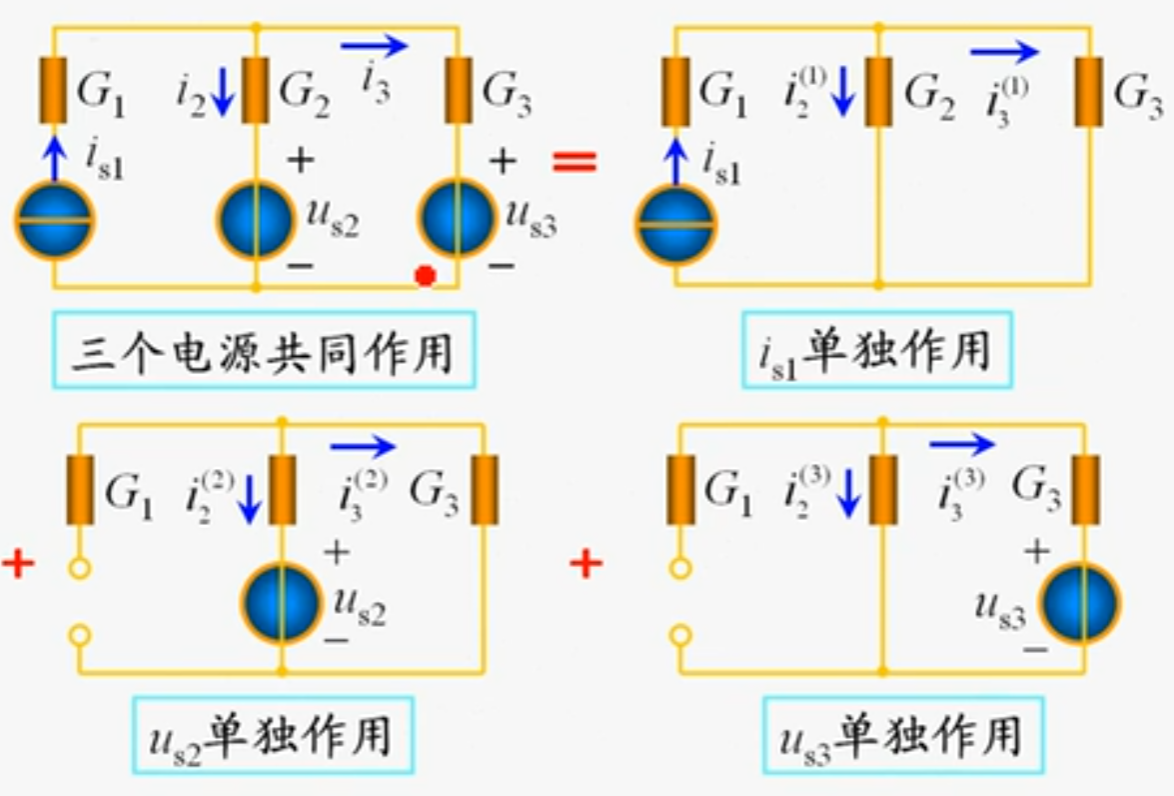
例:求电压源的电流及功率
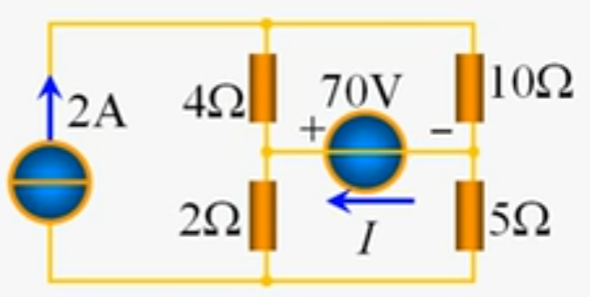
将上方电路进行拆分,拆分成两个简单电路的单独作用:
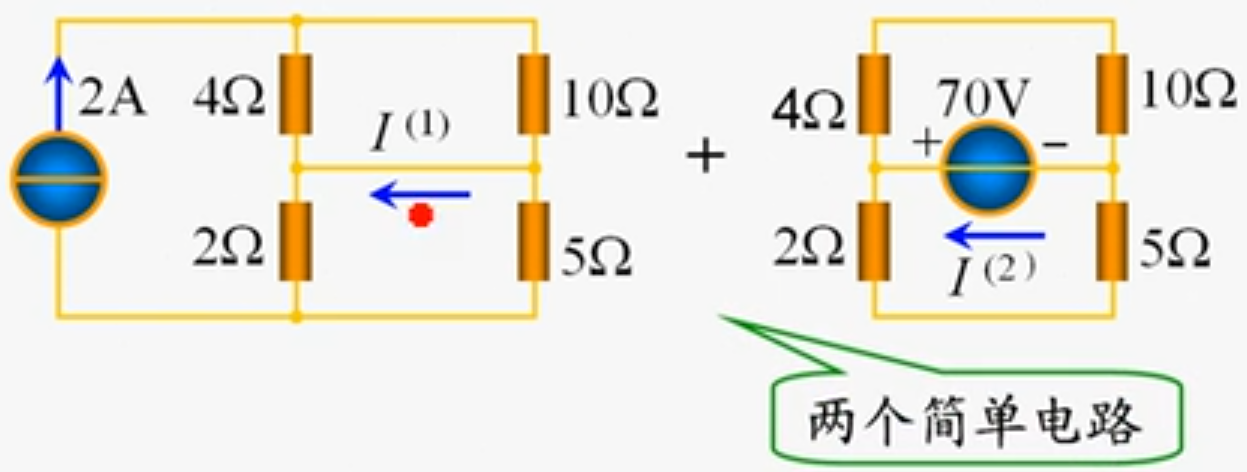
显然左边的图为电桥平衡状态,此时$I(1)=0$,右图在4Ω和2Ω间的结点列写KCL得$I(2)=70/14+70/7=15A$。所以原电路$I=I(1)+I(2)=15A,P_发=15\times 70=1050W$
齐性原理
线性电路中,所有激励(独立源)都增大(或减少)同样的倍数,则电路中响应(电压或电流)也增大(或减小)同样的倍数。
注:
- 当激励只有一个时,则响应与激励成正比。
- 具有可加性。
例:
$R_L=2Ω,R_1=1Ω,R_2=1Ω,u_s=51V$,求电流i。
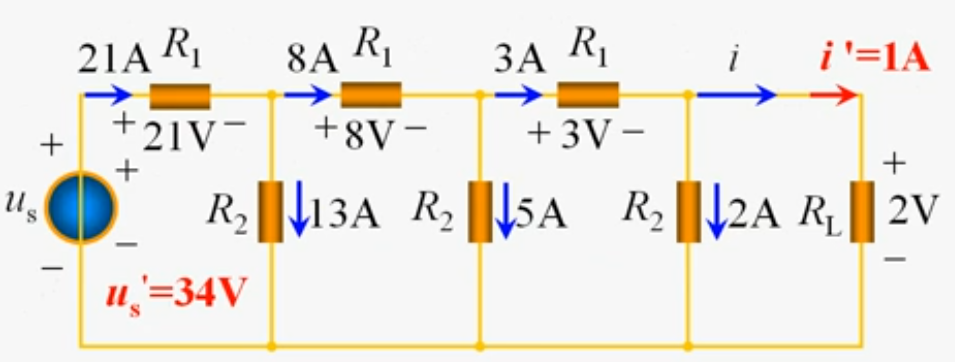
采用倒推法:设$i’=1A$
由齐性原理,则$\frac{i}{i’}=\frac{u_s}{u_s’}$,即
$$
i=\frac{u_s}{u_s’}i’=\frac{51}{34}\times 1 =1.5A
$$
替代定理
对于给定的任意一个电路,若某一支路电压为u,电流为i,那么这条支路就可以用一个电压等于u的独立电压源,或者用一个电流等于i的独立电流源,或用R=u/i的电阻来替代,替代后电路中全部电压和电流均保持原有值
例:
求图中电路的支路电压和电流
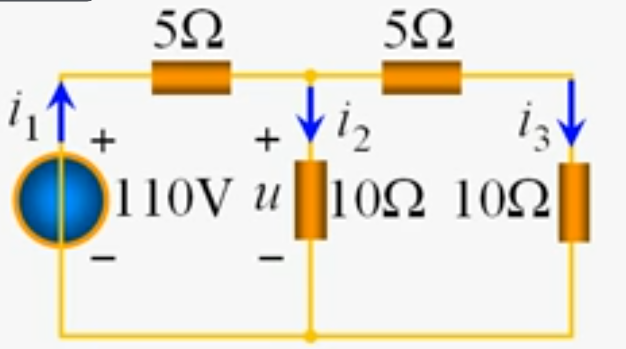
先用电阻等效算:
$$
i_1=\frac{110}{5+(5+10)//10}=10A
$$
并联分流算得$i_2=(15\times i_1)/10+15=6A,i_3=i_1-i_2=4A$,欧姆定律再得$u=6\times 10=60V$
用将上图用替代定理验证,可得
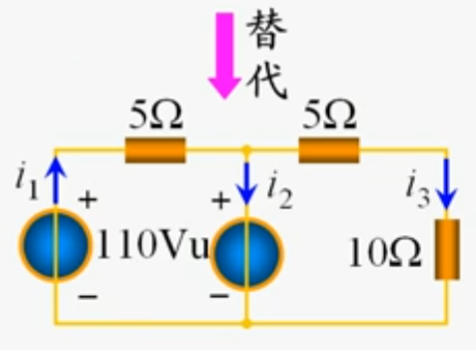
此时上方已经算得$V_u=60V$,则$i_1=(110-60)/5=10A,i_3=60/(10+15)=4A$
替代后各支路电压和电流完全不变。
戴维宁定理和诺顿定理
戴维宁定理和诺顿定理就是将要求部分的外端等效成电阻和电压源串联的形式,以此来求出要求部分的电压或电流。
定理的应用
开路电压$U_{oc}$的计算
戴维宁等效电路中电压源电压等于将外电路断开时的开路电压$U_{oc}$,电压源方向与所求开路电压方向有关。
等效电阻的计算
等效电阻将一端口网络内部独立源全部置零(电压源短路,电流源开路)后,所得无源一端口网络的输入电阻。(若有受控源可使用外加电源法,加电压求电流或加电流求电压)
通过戴维宁定理可将外部有源端口网络等效成如下图
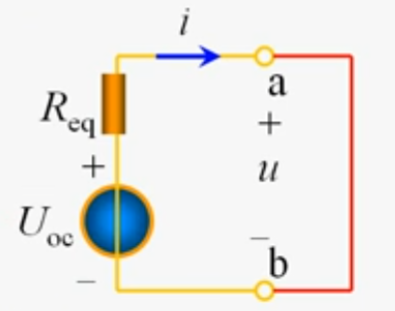
例:
求开路电压$U_{oc}$
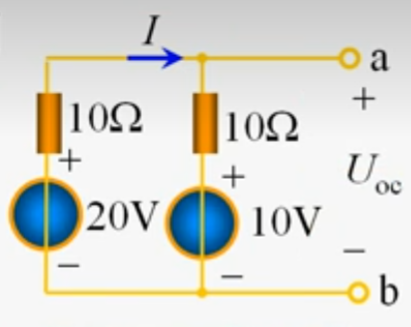
$$
I=\frac{20-10}{10+10}=0.5A\
U_{oc}=10+0.5\times 10 = 15V
$$
再求输入电阻$R_{eq}$,将电源都置零得$R_{eq}=10//10=5Ω$,所以可以等效为:
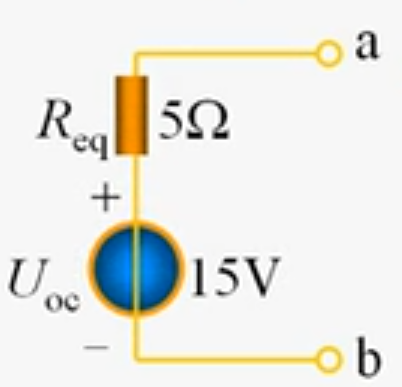
诺顿定理则是换成电流源,方向从电压源负到正。
注
- 外电路可以是任意的线性或非线性电路,外电路发生改变时,含源一端口网络的等效电路不变。
- 当一端口内部含有受控源时,控制电路与受控源必须包含在被化简的同一部分电路中
最大功率传输定理
一个含源线性一端口电路,当所接负载不同时,一端口网络传输给负载的功率就不同,讨论负载为何值时能从电路中获取最大功率。
最大功率传输定理就是用戴维宁来等效后再根据负载来算最大功率
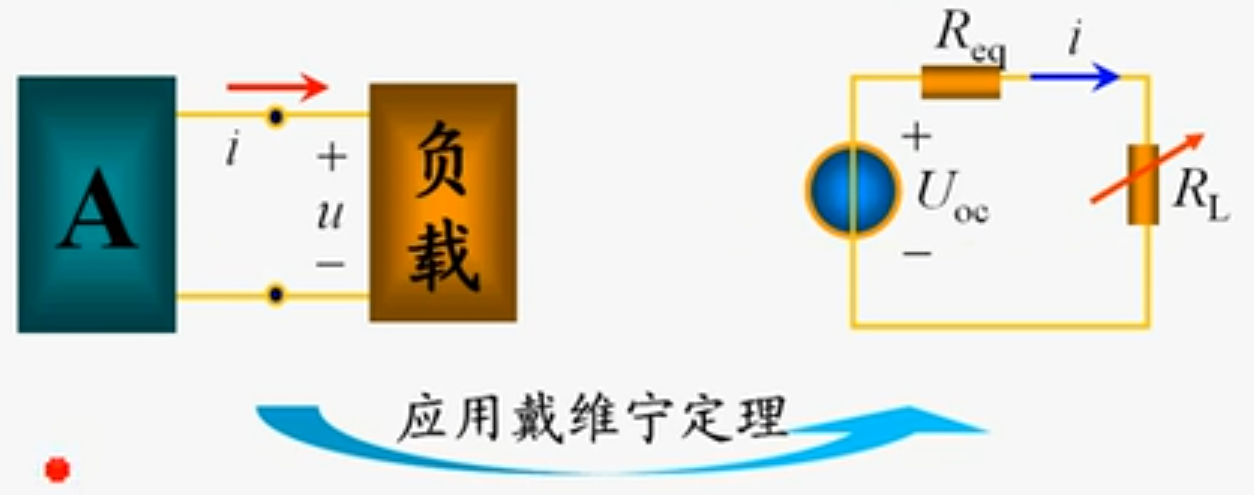
根据$P=R_L(\frac{u_{oc}}{R_{eq}+R_L})^2$($R_L$为未知量)可最后算得最大功率:
$$
R_L=R_{eq}时,P_{max}=\frac{u_{oc}^2}{4R_{eq}}
$$

