计算机组成原理-浮点数的表示与运算

浮点数的表示

由于定点数可表示的数字范围有限，而又不能无限制的增加数据的长度，就得考虑在位数不变的情况下增加数据的表示范围，以此拓展了浮点数。例，用定点数表示电子的质量($9 \times 10^{-28}g$)。

浮点数的表示格式

通常，浮点数表示为
$$
N=(-1)^S\times M \times R^E
$$
其中，S取值0或1，用来决定浮点数的符号；M是一个二进制定点小数，称为尾数，一般用定点原码小数表示，称为阶码或指数，用移码表示。R是基数（隐含），可以约定为2、4、16，基本为2等。

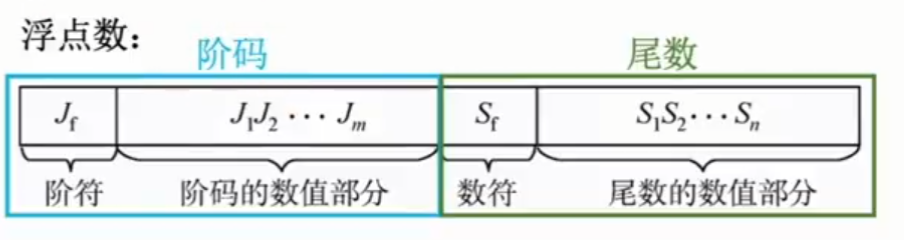
尾数的位数反映浮点数的精度。

例：阶码、尾数均用补码表示，求a、b的真值

$a=0,01;1.1001$，$b=0,10;0.01001$(阶码,前为符号位，尾数.前为符号位)

a: 阶码0,01 对应真值 +1 尾数 1.1001 对应原码 1.0111，对应真值为 -0.0111，所以a的真值$=2^1\times (-0.0111)=-0.111$

b: 阶码0,10 对应真值 +2 尾数 0.01001 对应真值 +0.01001 ，所以b的真值$=2^2\times (+0.01001)=+1.001$

浮点数的规格化

尾数的尾数决定浮点数的有效数位，有效数位越多，数据的精度越高。为了在浮点数运算过程中尽可能多的保留有效数字的位数，所以才需进行规格化操作。所谓规格化，是指通过调整一个非规格化浮点数的尾数和阶码的大小，使非零的浮点数在尾数的最高数位商保证是一个有效值。

• 左规：当浮点数运算的结果为非规格化要进行规格化处理，将尾数算数左移一位，阶码减1.
• 右规：当浮点数运算的结果尾数出现溢出（双符号位为01或10）时，尾数算数右移一位，阶码加1.

例： a = 010; 00.1100 , b = 010; 00.1000 , 求a+b

可得 a $= 2^2\times 00.1100$， b = $2^2 \times 00.1000$， a+b = $2^2\times(00.1100 + 00.1000)=2^2\times 01.0100$，此时就导致了溢出，可以通过右规得：a + b= $2^2\times 01.0100= 2^3\times 00.1010$

浮点数规格化的特点

1. 用原码表示的尾数进行规格化：

   1. 正数为$0.1\times \times \dots \times$的形式（0为符号位，最高位为1），其最大值表示为$0.1111\dots 1$；最小值表示为$0.100\dots 0$。尾数的表示范围$\frac{1}{2} \leq M \leq (1-2^{-n})$
   2. 负数为$1.1\times \times \dots \times$的形式，其最大值表示为$1.1000\dots0$；最小值表示为$1.1111\dots1$。尾数的表示范围为$-(1-2^{-n})\leq M \leq -\frac{1}{2}$

2. 用补码表示的尾数进行规格化：

   1. 正数为$0.1\times \times \dots \times$的形式（0为符号位，最高位为1），其最大值表示为$0.1111\dots 1$；最小值表示为$0.100\dots 0$。尾数的表示范围$\frac{1}{2} \leq M \leq (1-2^{-n})$
   2. 负数为$1.0\times \times \dots \times$的形式，其最大值表示为$1.0111\dots 1$；最小值表示为$1.000\dots0$。尾数的表示范围为$-1\leq M \leq -(1/2 +2^{-n})$

   总结：

   规格化的原码尾数，最高数值位一定是1，规格化的补码尾数，符号位与最高数值位一定相反。

例：若某浮点数的阶码、尾数用补码表示，共4+8位； 0.110; 1.1110100，进行规格化：

由于补码负数的最高位和符号位要相反，所以要进行左规进行规格化，$2^6\times -(1110100)=2^3 \times -(01000000)$，就规格化完毕。

基数不同，浮点数的规格化形式也不同。

浮点数 IEEE 754标准

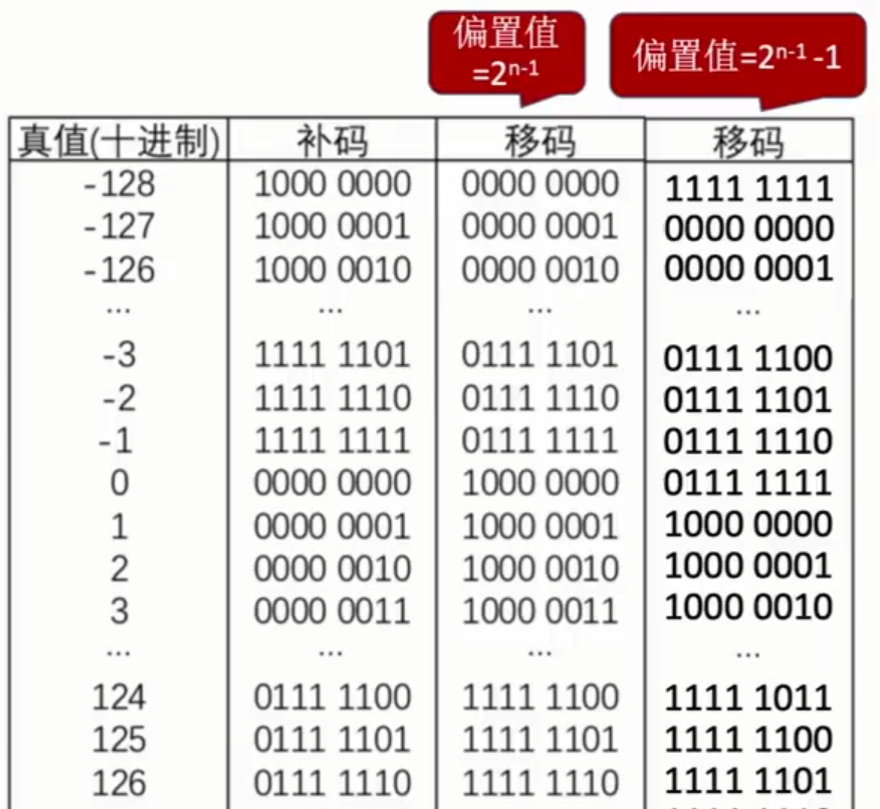
在了解IEEE 754标准前，先回忆下移码的概念，移码实际就是补码的符号位取反获得。移码的定义是：移码=真值+偏置值（偏置值一般是$2^{n-1}$，此时移码=补码符号位取反）。

例：设8位机器来表示移码，此处8位移码的偏置值=128D=1000 0000B。

真值 -127D = -1111 111B，移码 = -111 1111 + 1000 0000= 0000 000

在IEEE 754标准中，通常会将偏置值=$2^{n-1}-1$

IEEE754标准规定常用的浮点数格式有短浮点数（单精度、float型）、长浮点数（双精度、double型）、临时浮点数，其基数隐含为2，在IEEE754中，尾数采用原码表示。

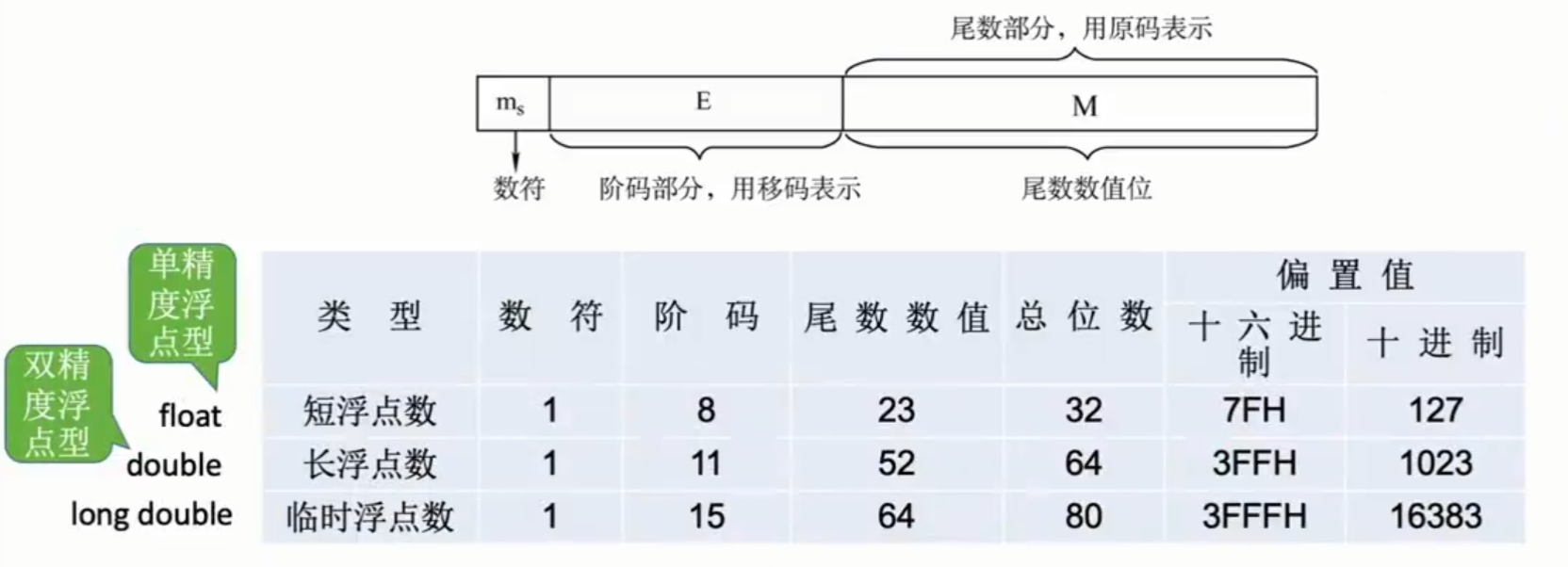
由于移码=真值+偏置值，由此可以得出阶码真值=移码-偏移量

规格化的短浮点数的真值为：$(-1)^s\times 1.M\times 2^{E-127}$

规格化长浮点数的真值为：$(-1)^s\times 1.M\times 2^{E-1023}$

例：将十进制数-0.75转换为IEEE754的单精度浮点数格式表示

由于是负数，所以数符=1，尾数部分=.100000….（共23位，隐含最高位1），移码=真值+偏置值=-1+127=-1 + 111 1111 = 0111 1110（凑足8位）

最后可得IEEE 754标准规定浮点数为：1011 1111 0100 0000 0000 0000 0000 0000

例2：IEEE 754的单精度浮点数 C0 A0 00 00 H的值是多少

C0 A0 00 00 -> 1100 0000 1010 0000 0000 0000 0000 0000，可得数符=1，所以为负数，尾数部分=1.01，真值=移码 - 偏置值= 1000 0001 - 0111 1111 = 0000 0010 = 2D，所以最终值为$(-1.01)_2\times2^2=(-1.25)\times2^2=-5.0$

IEEE 754单精度浮点型能表示的最小绝对值、最大绝对值

最小绝对值：尾数全为0，阶码真值最小 -126（**-128全1和-127全0有其他用途**），对应移码机器数 0000 0001 此时整体的真值为$(1.0)_2\times 2^{-126}$。

最大绝对值：尾数全为1，阶码真值最大 127，对应移码机器数 1111 1110 此时整体的真值为$(1.111..11)_2\times 2^{127}$。

只有$1\leq E \leq 254 $时，真值=$(-1)^s\times 1.M \times 2^{E-127} $

当阶码全为0，尾数M不全为0时，表示非规格小数，则真值表示形式为$±(0.xxx…x)_2 \times 2^{-126}$

阶码真值固定为-126。

当阶码全为0，尾数M全为0时，表示真值±0

当阶码全为1，尾数M全为0时，表示真值无穷大$±\infin$

当阶码全为1，尾数M不全为0时，表示真值非数值“NaN”（Not a Number）

定点、浮点表示的区别

1. 数值的表示范围

   若定点数和浮点数的字长相同，则浮点表示法所能表示的数值范围远大于定点表示法。

2. 精度

   对于字长相同的定点数和浮点数来说，虽然浮点数扩大了表示范围，但精度降低了。

3. 数的运算

   浮点数包括阶码和尾数两部分，运算时不仅要左尾数的运算，还要做阶码的运算，而且运算结果要求规格化。

4. 溢出问题

   在定点数运算中，当运算结果超出数的表示范围时，发生溢出；浮点运算中，运算结果超出尾数表示范围却不一定溢出，只有规格化后阶码超出所能表示的范围时，才发生溢出。

浮点数的加减运算

浮点数加减运算分为以下几步：

1. 对阶
2. 尾数加减
3. 规格化
4. 舍入
5. 判溢出

例：已知十进制数$X=-5/256$、$Y=+59/1024$，按机器补码浮点运算规则计算 X - Y，结果用二进制表示，浮点数格式如下：阶符取2位，阶码取3位，数符取2位。尾数取9位。

将X，Y用二进制表示$X=(-101)_2\times2^{-8}=(-0.101)_2\times2^{-5}$

$Y=(+111011)_2\times 2^{-10}=(0.111011)_2\times 2^{-4}$

由题目用补码表示X和Y，且阶乘也用二进制补码形式，则有（阶符取2位，阶码3位）：

X=$(11.011000000)_{补}\times 2^{11011}$

Y=$(00.111011000)_补\times 2^{11100}$

最后进行组合则有

X=$11011,11.011000000$

Y=$11100,00.111011000$

1. 对阶

   首先要将阶码对齐，阶数小的对阶数大的对阶，尾数每右移一位，阶码加1。

   计算机判断哪个阶数大，通过求阶差：$[ΔE]_补=11011 + 00100=11111$ ，得ΔE=-1，说明X比Y阶数小，且小1，需要让X尾数右移。得$X=11100,11.101100000$

2. 尾数加减

   将对阶后的值尾数进行相减：

   $X-Y=11100,11.101100000 + 11100,11.000101000=11100,10.110001000$

3. 规格化

   $X-Y:11100,10.110001000$ -> $X-Y:11101,11.011000100$

4. 舍入

   无舍入

5. 判溢出

   常阶码，无溢出，结果真值为$2^{-3} \times (-0.1001111)_2$（若阶码上溢，直接抛出异常终端，阶码下溢出，则按机器0处理）

舍入方法

“0”舍“1”入法

类似于十进制数中的“四舍五入”，即在尾数右移时，被移去的最高数位为0，则舍去；若为1，则在尾数的末位加1。这可能会使尾数又溢出，此时需要再做以此右规。

恒置“1”法

尾数右移时，不论丢掉的最高数值位是“1”还是“0”，都使右移后的尾数末位恒置“1”。这种方法同样有使尾数变大或变小的可能。

强制类型转换

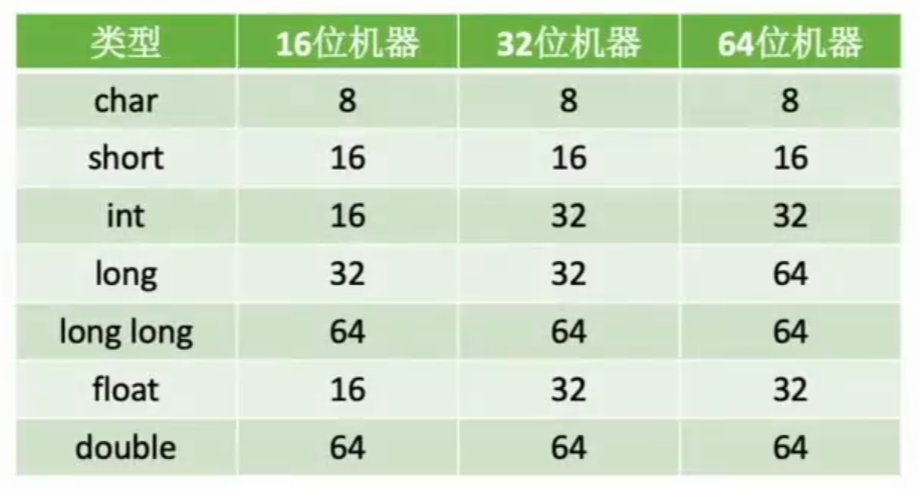
上表为C语言在各机器中所占大小，当强制类型转换以 char -> int -> long -> double和 float -> double时，范围都由小到大，精度不会丢失。（long->double是以32位机器位标准，64位会出现精度损失）

int可以表示32位，float表示为 1 + 8 + 23 = 32，实际能表示的数为24位（23+1包含隐含的1）。所以int转float会产生精度损失，但不会溢出。 而float->int，可能溢出及损失精度。