网孔电流法
网孔电流法是以沿网孔连续流动的假想电流为未知量列写电路方程分析电路的方法。仅适用于平面电路。
基本思想:
为减少未知量的个数,假想每个回路种有一个回路电流。各支路电流可用回路电流的线性组合表示,来求得电路的解。
列写的方程:
网孔电流在网孔中是闭合的,对每个相关节点均流进一次,流出一次,所以KCL自动满足。因此网孔电流法的方程个数即为网孔数。网孔方程是根据KVL进行列写。
例:
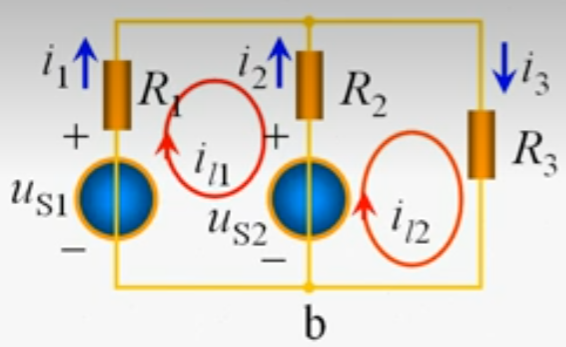
假想图1-1两个回路$l_1,l_2$的电流分别为$i_{l1},i_{l2}$,支路电流可表示为:
$$
i_1=i_{l1}\qquad i_3=i_{l2}\
i_2=i_{l2} - i_{l1}
$$
方程可列写为:
$$
\begin{cases}
\ l_1:R_1i_{l1}+R_2(i_{l1}-i_{l2})+u_{S2}-u_{S1}=0\
\ l_2:R_2(i_{l2}-i_{l1})+R_3i_{l2}-u_{S2}=0\
\end{cases}
$$
整理得:
$$
\begin{cases}
\ l_1:(R_1+R_2)i_{l1}-R_2i_{l2}=u_{S1}-u_{S2}\
\ l_2:-R_2i_{l1}+(R_2+R_3)i_{l2}= u_{S2}\
\end{cases}
$$
若称回路自身所经过的电阻为自电阻,与其他回路共有的称为互电阻。
由上方方程可得自身回路电流为自电阻之和,若支路方向相同时,互电阻取正号,相反时取负号并乘上对方的回路电流。
网孔电流法的一般步骤:
- 选网孔为独立回路,并确定其绕行方向;
- 以网孔电流为未知量,自动满足KCL,列其KVL方程,且是独立的;
- 求上诉方程,得到l个网孔电流;
- 求各支路电流;
- 其他分析;
回路电流法
回路电流法是网孔电流法的拓展,以基本回路中沿回路连续流动的假想电流为未知量列写电路方程分析电路的方法。适用于平面和非平面方程。
例:
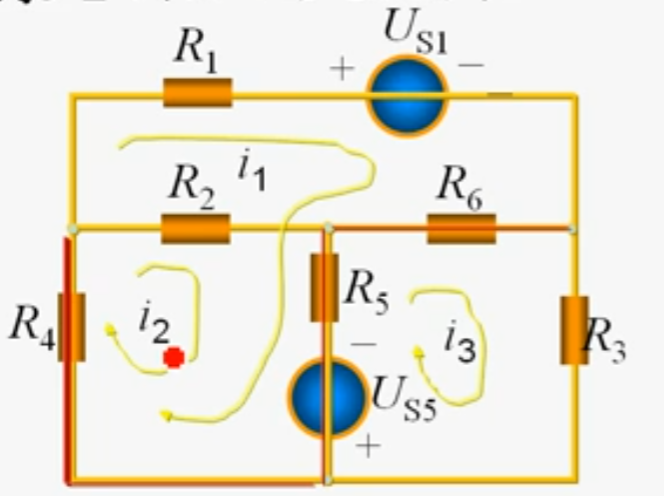
如图1-2中选取回路电流为$i_1,i_2,i_3$,可根据网孔电流法列出相应的回路电流方程:
$$
\begin{cases}
\ l_1:(R_1+R_6+R_5+R_4)i_1+(R_5+R_4)i_2-(R_5+R_6)i_3=-u_{S1}+u_{S5}\
\ l_2:(R_5+R_4)i_1+(R_2+R_5+R_4)i_2-R_5i_3=U_{S5}\
\ l_3:-(R_5+R_6)i_1-R_5i_2+(R_3+R_5+R_6)i_3=-u_{S5}
\end{cases}
$$
结点电压法
以结点电压为未知量列写电路方程分析电路的方程。适用于结点较少的电路
基本思想
选结点电压为未知量,则KVL自动满足,无需列写KVL方程。各支路电流、电压可视为结点电压的线性组合,求出结点电压后,便可得到各支路电压、电流。
方程的列写
结点电压列写的是结点上KCL方程。
- 选定参考结点,表明其余n-1个独立结点的电压。
- 列写KCL方程:$\sum i_{R出}=\sum i_{S入}$
例:
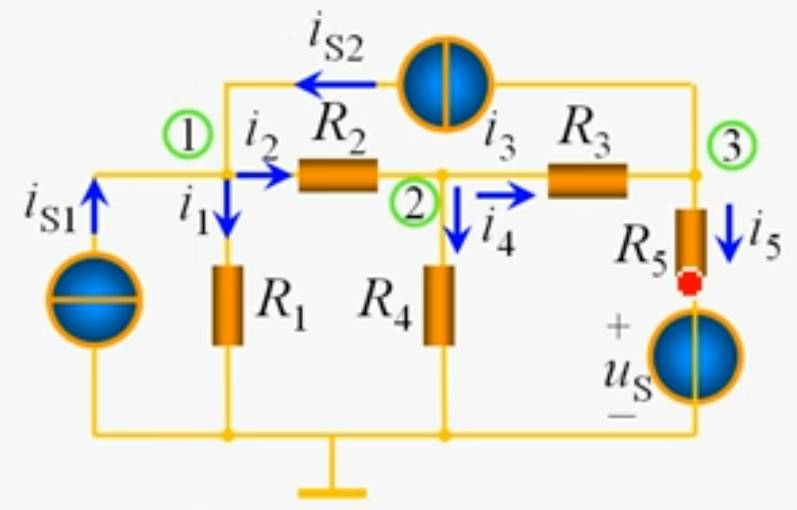
将最下方接地,1 2 3号结点电压为$u_{n1}u_{n2}u_{n3}$列1 2 3号结点的KCL方程:
$$
1 :i_1+i_2=i_{s1}+i_{s2}\
2 :-i_2+i_3+i_4=0\
3 :-i_3+i_5=-i_{s2}
$$
然后把支路电流用结点电压表示:
$$
\frac{u_{n1}}{R_1}+\frac{u_{n1}-u_{n2}}{R_2}=i_{s1}+i_{s2}\
-\frac{u_{n1}-u_{n2}}{R_2}+\frac{u_{n2}-u_{n3}}{R_3}+\frac{u_{n2}}{R_4}=0\
-\frac{u_{n2}-u_{n3}}{R_3}+\frac{u_{n3}-u_s}{R_5}=-i_{s2}
$$
最后整理得:
$$
\begin{cases}
(\frac{1}{R_1}+\frac{1}{R_2})u_{n1}-(\frac{1}{R_2})u_{n2}=i_{s1}+i_{s2}\
\ -(\frac{1}{R_2})u_{n1} +(\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4})u_{n2}-(\frac{1}{R_3})u_{n3}=0\
\ -(\frac{1}{R_3})u_{n2}+(\frac{1}{R_3}+\frac{1}{R_5})u_{n3}=-i_{s2}+\frac{u_s}{R_5}
\end{cases}
$$
即为结点电压的最终方程表达式(或者用电导的形式)
根据上方例子可总结出结点电压法的特性:
设$\frac{1}{R_i}=G_i$(电阻的倒数等于电导),那么该结点的自电导(即与该结点相邻的电导)之和与该结点电压相乘,互电导(互电导为接在结点与结点之间的电导之和)总为负值

