计算机组成原理-数据的表示与运算

计算机组成原理 数制与编码
计算机组成原理
发布日期:   2023-11-21
更新日期:   2023-11-29
文章字数:   8.8k

数制与编码

进位计数制及其相互转换

总所周知，计算机系统内部只能使用二进制进行编码，所以进制间的转换尤为重要。

进位计数法

常用的进位计数法由十进制、二进制、八进制、十六进制等。

  1. 二进制：二进制只有0和1两种数字符号，计数“逢二进一”，它的任意数位权位$2^i$，i位所在位数。
  2. 八进制：八进制有0~7八种数字符号，计数“逢八进一”，它的任意数位权位$8^i$，i位所在位数，二进制的3位数码编为一组解释一位八进制数码。
  3. 八进制：八进制有0~9、A、B、C、D、E、F十六种符号，计数“逢十六进一”，它的任意数位权位$16^i$，i位所在位数，二进制的4位数码编为一组解释一位十六进制数码。
各种进制的常见书写方式：
  1. 二进制： $(1010)_2=1010B$
  2. 八进制：$(1652)_8$
  3. 十六进制：$(1652)_{16}=1652H=0x1652$
  4. 十进制：$(1652)_{10}=1652D$
不同进制数间的相互转换

  1. 二进制转换八进制数和十六进制数

    在进行转换时，应以小数点为界。3位（4位）二进制转为1位八进制（十六进制），若整数不足3位（4位）则需在左侧补0补齐位数，而若浮点数部分不足3位（4位）则需在右侧补0齐位数。

    例：将1111000010.01101分别转换为八进制和十六进制数。

    解：

    转八进制
    $$
    (1111000010.01101)_2 =(001\ 111\ 000\ 010.011\ 010)_2\
    =(1702.32)_8
    $$
    转十六进制
    $$
    (1111000010.01101)_2 =(0011\ 1100\ 0010.0110\ 1000)2\
    =(3C2.68)    {16}
    $$
    同样，由八进制（十六进制）转二进制，只需将每位改成2位（4位）二进制数即可。

  2. 任意进制转十进制数

    将任意进制数的各位数码与它们的权值相乘，再把乘积相加即可得到对应的十进制数。

    例：$(11011.1)_2$转为十进制：
    $$
    (11011.1)2=1\times 2^4 + 1\times 2^3 +0\times 2^2 + 1\times 2^1 + 1 \times 2^0 + 1 \times 2^{-1} = (27.5){10}
    $$

  3. 十进制数转换为任意进制数

    一个十进制数转换为任意进制数，常用基数乘除法，即对整数部分用除基取余法，对小数部分用乘基取余法，最后将整数部分和小数部分的转换结果拼接即可。

    例：$(75.3)_{10}$转二进制：

    整数部分计算（“…”后面为余数）：
    $$
    75\div 2=37\dots1\
    37\div 2=18\dots1\
    18\div 2=9\dots0\
    9\div 2=4\dots1\
    4\div 2=2\dots0\
    2\div 2=1\dots0\
    1\div 2=0\dots1\
    $$
    下面为高位，上面为低位，可得整数部分二进制为$(75)_{10}=(1001011)_2$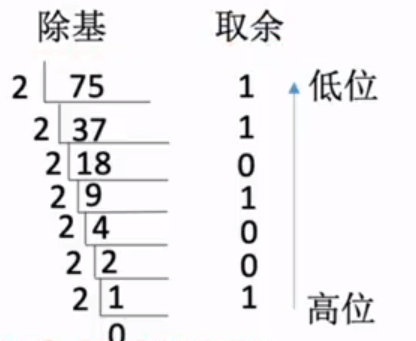

    1-1

    小数部分$(0.3){10}$计算：
    $$
    0.3\times 2= 0.6 = 0 + 0.6\
    0.6\times 2= 1.2 = 1 + 0.2\
    0.2\times 2= 0.4 = 0 + 0.4\
    0.4\times 2= 0.8 = 0 + 0.8\
    0.8\times 2= 1.6 = 1 + 0.6\
    \dots
    $$
    小数部分无法精确转换，到出现相同值即可$(0.3)    {10}=(01001\dots)_2$

    1-2

所以$(75.3)_{10}=(1001011.01001\dots)_2$

真值和机器数

日常生活中，通常用正号、负号来表示正数和负数，如+15、-8等。这种带“+”或“-”符号的数称为真值。真值是机器数所代表的实际值。

在计算机中，通常用“0”表示“正”，“1”表示“负”。这种把符号“数字化”的数称为机器数。常用的由源码、补码和反码表示。例：0,101（”,”区分符号位与数值位）表示+5。

BCD(Binary-Coded Decimal)码

二进制编码的十进制通常用4位二进制数来表示一位十进制中的0~9这10个数码。可得必有6种状态为冗余状态。

常用的BCD码：

  1. 8421码（常用）：它是一种有权码，设其各位的数值为$b_3,b_2,b_1,b_0$，则权值从高到低依次为8,4,2,1，它表示的十进制数为$D=8b_3+4b_2+2b_1+1b_0$。如 8->1000; 9->1001;

    若两个8421码相加之和大于或等于$(1010)2$，即$(10){10}$，则需要加6修正（从1010到1111这6个无效码），并向高位进位。

    例：$(0100){8421}+(1001){8421}=(1101){8421}$，即$4+9=13$需要进行修正：
    $$
    (1101)    {8421}+(0110)_{8421}=(10011)_2
    $$

  2. 余3码：它是一种无权码，是在8421码的基础上加$(0011)_2$形成的，因每个数都多余”3“，因此称为余3码。如8->1011; 9->1100。

  3. 2421码：它是一种有权码，权值由高到低分别为2，4，2，1，特点是大于或等于5的4位二进制数中最高位为1，小于5的最高位为0。

定点数的编码表示

根据小数点的位置是否固定，在计算机中有两种数据格式：定点表示和浮点表示。

定点数：即小数点位置固定。例：996.007 （小数点位置会随数的大小发生变化）

浮点数：即小数点的位置不固定。 例：$9.96007\times 10^2$ （小数点位置不会随数的大小发生变化，科学计数法）

机器数的定点表示

无符号数：无符号数就是整个机器字长全部二进制位均为数值位，没有符号位，相当于数的绝对值。

无符号数表示范围（通常只有无符号整数，而没无符号小数）：

​ 若有8位二进制数：则有$2^8$种不同的状态，即$(0000\ 0000)_2\ $$ (1111\ 1111)_2$，十进制为0255种状态。

​ 可得n位的无符号数的表示范围：0~$2^n-1$

有符号数的定点表示法用来表示定点小数和定点整数。

  1. 定点小数：即约定符号位之后、有效数值最高位前位小数点位置，就是符号位后就是小数部分。
  2. 定点整数：即在整数部分最低位之后为小数点。

1-3

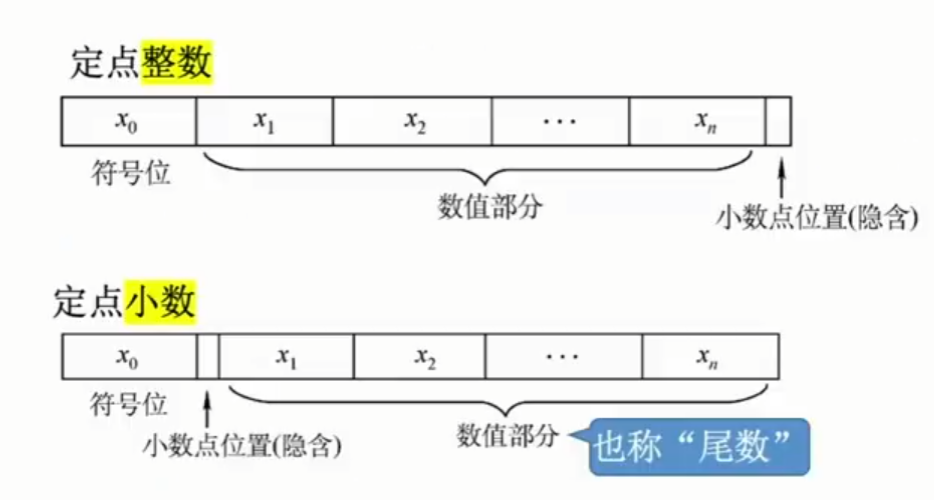
注：可用原码、反码、补码三种表示定点整数和定点小数，可用移码来表示定点整数。

若真值为x，则用$[x]_原、[x]_反、[x]_补、[x]_移$分别表示对应的原、反、补、移码。

原码、补码、反码、移码

原码表示法

用机器数的最高位表示数的符号，其余各位表示数的绝对值。

例：机器字长为8位，那么最高位为符号位，剩下7位为数的有效位。

定点整数的原码表示：

1-4

若存入的值是$+19D$，那么此时存储的二进制为$[x]_原=0,0010011$。

若存入的值是$-19D$，那么此时存储的二进制为$[x]_原=1,0010011$。

此时小数点默认隐含在最低位的右边。

定点小数的原码表示：

1-5

若存入的值是$+0.75D$，那么此时存储的二进制为$[x]_原=0.1100000$。

若存入的值是$-0.75D$，那么此时存储的二进制为$[x]_原=1.1100000$。

此时小数点默认隐含在最低位的右边。

**可得若机器字长为n+1位，则尾数占n位。 **

原码整数的表示范围：$-(2^n-1)\leq x \leq 2^n-1 $。真值0有**+0和-0**两种形式。

原码小数的表示范围：$-(1-2^{-n})\leq x \leq 1-2^{-n} $。真值0有**+0和-0**两种形式。

反码表示法

若符号位为0（即为正数），则反码与原码相同。

若符号位为1（即为负数），则数值位全部取反则为反码。

例：
$$
x=+19D \quad [x]_原=0,0010011\
\qquad [x]_反=0,0010011\
x=-19D \quad [x]_原=1,0010011\
\qquad [x]_反=1,1101100\
x=+0.75D \quad [x]_原=0.1100000\
\qquad [x]_反=0.1100000\
x=-0.75D \quad [x]_原=1.1100000\
\qquad [x]_反=1.00111111\
$$
若机器字长n+1位，

反码整数的表示范围：$-(2^n-1)\leq x \leq 2^n-1 $。真值0有**+0和-0**两种形式。

反码小数的表示范围：$-(1-2^{-n})\leq x \leq 1-2^{-n} $。真值0有**+0和-0**两种形式。

补码表示法

若设机器字长为8位，那么计算机会自动完成$mod\ 2^8$的运算，可以通过补码来让加法操作实现减法操作，来节省硬件成本。

若符号位为0（即为正数），则补码与原码相同。

若符号位为1（即为负数），则在反码基础上末位+1（要考虑进位）。

例：
$$
x=+19D \quad [x]_原=0,0010011\
\qquad [x]_反=0,0010011\
\qquad [x]_补=0,0010011\
x=-19D \quad [x]_原=1,0010011\
\qquad [x]_反=1,1101100\
\qquad [x]_补=1,1101101\
x=+0.75D \quad [x]_原=0.1100000\
\qquad [x]_反=0.1100000\
\qquad [x]_补=0.1100000\
x=-0.75D \quad [x]_原=1.1100000\
\qquad [x]_反=1.00111111\
\qquad [x]_补=1.01000000\
$$

补码的真值0只有一种表示形式

定点整数补码$[x]_补=1,0000000$表示$x=-2^7$。

若机器字长n+1位，

补码整数的表示范围：$-2^n\leq x \leq 2^n-1 $。

定点小数补码$[x]_补=1,0000000$表示$x=-1$。

补码小数的表示范围：$-1\leq x \leq 1-2^{-n} $。

移码表示法

移码是补码的基础上将符号位取反即可。注意：移码只能用于表示整数
$$
x=+19D \quad [x]_原=0,0010011\
\qquad [x]_反=0,0010011\
\qquad [x]_补=0,0010011\
\qquad [x]_移=1,0010011\
x=-19D \quad [x]_原=1,0010011\
\qquad [x]_反=1,1101100\
\qquad [x]_补=1,1101101\
\qquad [x]_移=0,1101101\
$$
若机器字长n+1位，

移码整数的表示范围：$-2^n\leq x \leq 2^n-1 $（与补码相同）。

使用移码表示的整数很方便的可以进行对比大小，移码通常用于表示阶码，不用来表示定点小数。

运算方法和运算电路

基本运算部件

一位全加器

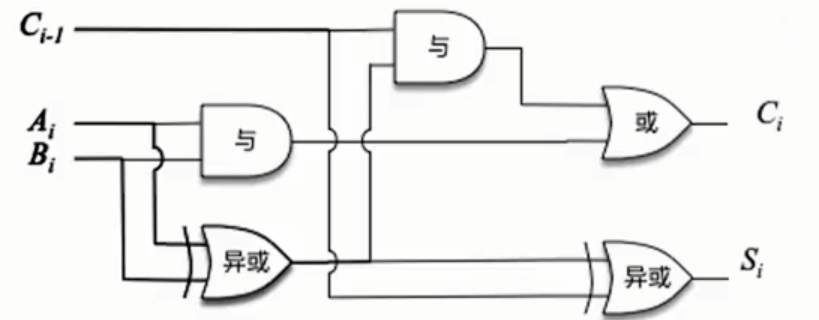
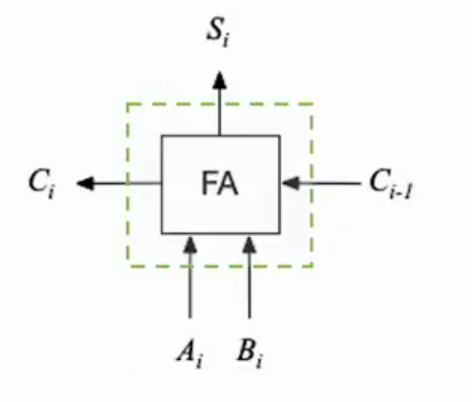
全加器（FA，Full Adder）是最基本的加法单元，有加数$A_i$、加数$B_i$与低位传来的进位$C_{i-1}$共三个输入，有本位和$S_i$与向高位进位$C_i$共两个输出。全加器的逻辑表达式如下：

和表达式：$S_i=A_i⊕B_i⊕C_{i-1}$（$A_i、B_i、C_{i-1}$中有奇数个1时，$S_i=1$；否则$S_i=0$）

进位表达式：$C_i=A_iB_i+(A_i⊕B_i)C_{i-1}$

全加器逻辑结构图：

2-1

逻辑符号：

2-2

n串行进位加法器

把n各全加器相连可得到n位加法器，称为串行进位加法器，如图2-3所示。串行进位又称行波进位，每级进位直接依赖于前一位的进位。

2-3

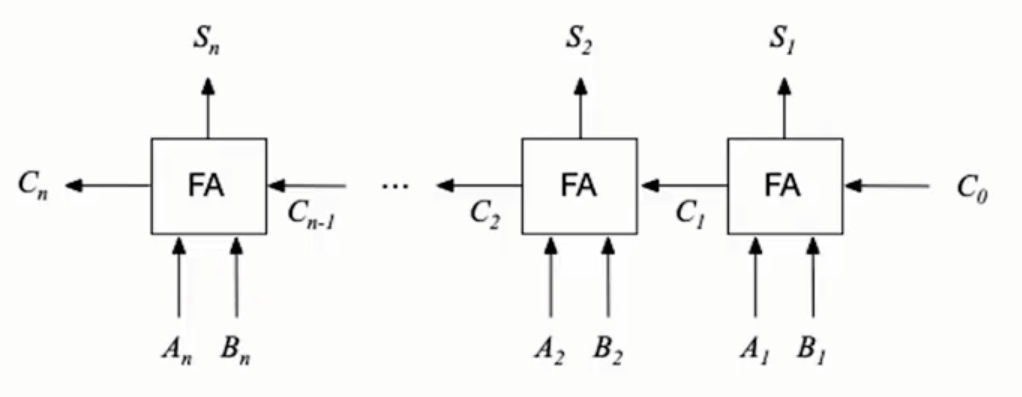
将n位加法器进行封装，则可得到图2-4.

2-4

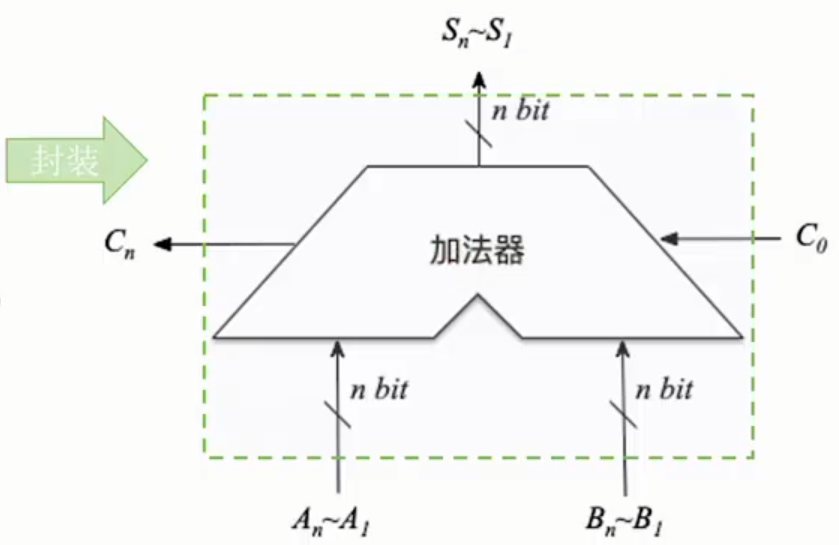
在串行进位加法器中，依赖前一位的进位导致计算速度取决于进位产生和传递的速度。位数越多，运算速度越慢。

并行进位加法器

由于串行进位加法器依赖前一位的进位会导致速度变慢，要解决就可以通过在产生进位时用CLA部件来接受进位信息，从而达到并行进位的效果。

2-5

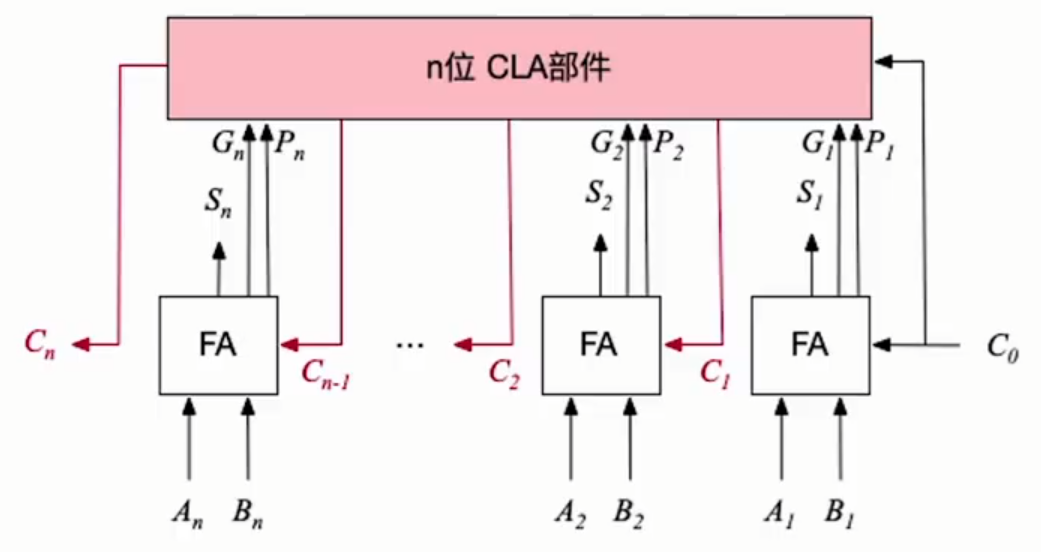
由于所有信息都是同时产生的，运行速度会比“串行进位加法器”更快。

并行加法器可以通过串行加法器以下式子来推出：
$$
C_i=A_iB_i+(A_i⊕B_i)C_{i-1}\
C_{i-1}=A_{i-1}B_{i-1}+(A_{i-1}⊕B_{i-1})C_{i-2}\
C_{i-2}=A_{i-2}B_{i-2}+(A_{i-2}⊕B_{i-2})C_{i-3}\
\dots \
C_1=A_{1}B_{1}+(A_{1}⊕B_{1})C_{0}
$$
串行加法器中迟早会从$C_i$中展开到$C_0$。

根据上方$C_i$就可以等于：
$$
C_i=A_iB_i+(A_i⊕B_i)C_{i-1}（C_{i-1}用上方式子来替代）\
C_i=A_iB_i+(A_i⊕B_i)(A_{i-1}B_{i-1}+(A_{i-1}⊕B_{i-1})C_{i-2})\
C_i=A_iB_i+(A_i⊕B_i)(A_{i-1}B_{i-1}+(A_{i-1}⊕B_{i-1})(A_{i-2}B_{i-2}+(A_{i-2}⊕B_{i-2})C_{i-3}))\
\dots
$$
而$A_i、B_i、A_{i-1}、B_{i-1}\dots A_0,B_0$和$C_0$的数据在一开始就已经获取到了，因此就可以无需等算出进位在进行下一步，可以直接根据前方数据来算出相应的进位值。相应的要算越后面的进位则电路设计越复杂，一般实际应用中会算到第4位的进位值即可，如下图所示。

CLA

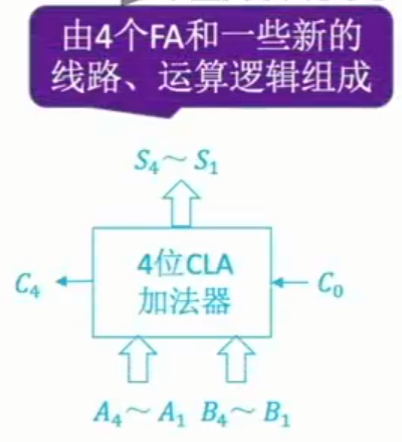
带标志加法器

无符号数加法器只能用于两个无符号数相加，不能进行带符号整数的加减运算。为了能进行带符号整数的加减运算，还需要在无符号数加法器的基础上增加相应的逻辑门电路，使得加法器不仅能进行加减运算，还能生成相应的标志信息。

2-6

在图2-4的基础上，增加标识位，这样就能实现带标志的加法器图2-6。

各标志的意义为：

  • OF(Overflow Flag)：溢出标志，用于判断带符号数加减运算是否溢出。OF=1 溢出； OF=0 未溢出
  • SF(Sign Flag)：符号标志，用于判断带符号数加减运算结果的正负性。SF=1 结果为负； SF=0 结果为正
  • ZF(Zero Flag)：零标志，用于判断加减运算结果是否为0。ZF=1 表示结果为0； ZF=0 表示结果不为0
  • CF(Carry Flag)：进位/借位标志，用于判断无符号数加减运算是否溢出。CF=1 溢出； CF=0 未溢出

各标志的逻辑表达式：

  • $OF=C_n⊕C_{n-1}$——最高位的进位同或次高位的进位。反映带符号数加减运算是否溢出。

  • $SF=S_n$——也就是取运算结果的最高位（符号位）。反映带符号数加减运算的正负性。

  • $ZF=\overline{S_n+\dots+S_2+S_1}$——仅当运算结果所有bit全0时，ZF才为1，此时表示运算结果为0。

  • $CF=C_{out}⊕C_{in}=C_n⊕C_0$——反映无符号数加减运算是否溢出。

各标志的逻辑图：

2-7

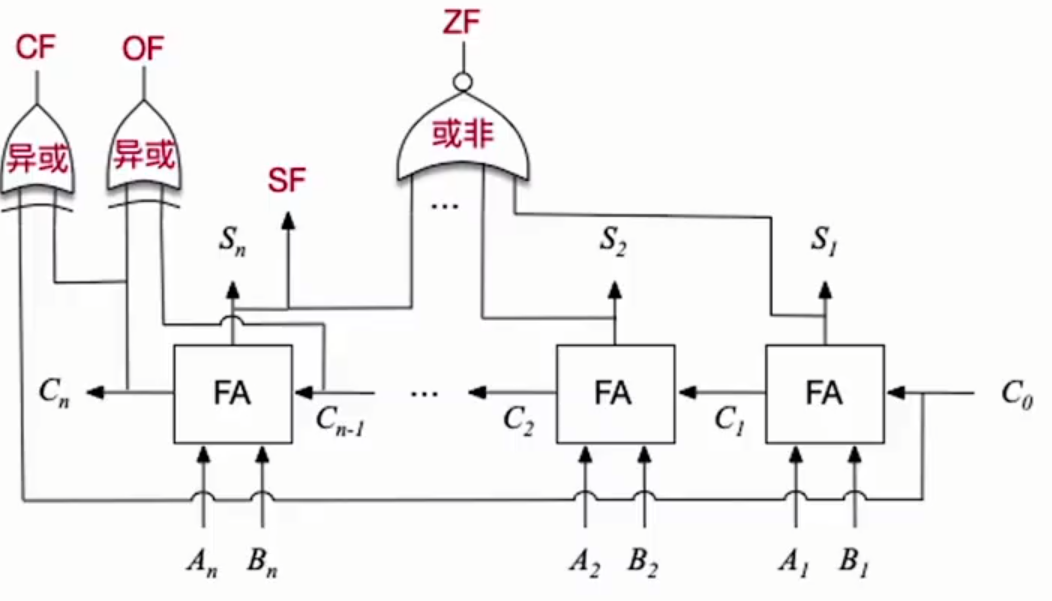
算数逻辑单元（ALU，Arithmetic and Logic Unit）

ALU是一种功能较强的组合逻辑电路，它能进行多种算数运算和逻辑运算。ALU的核心是带标志加法器，同时也能执行“与” “或” “非”等逻辑运算。

2-8

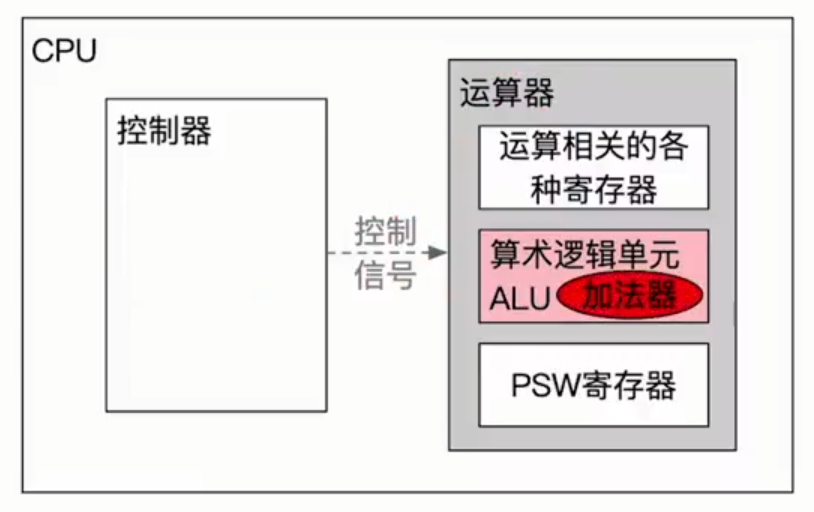
CPU想进行运算时，会通过控制器来解析指令，并根据指令功能发出相应的控制信号。然后运算器会对数据进行处理，此时就会通过ALU来进行运算，因此ALU是运算器的核心，而由于加减乘除等运算都基于“加法”来实现，因此加法器是ALU的核心。

2-9

若将图2-9进行封装，不显示细节，并添加几个标志位，可得下图2-10.

2-10

ALU有以下几个需要注意点：

  • 如果ALU支持k种功能，则控制信号位数$m\geq [\log_2k]$
  • ALU的运算数、运算结果位数与计算机的机器字长相同。
  • ZF/OF/SF/CF 标志位，用于表示本次运算结果的特征（ZF表示运算结果是否为零、OF表示有符号数运算结果是否溢出、SF表示有符号数运算结果的正负性、CF表示无符号数运算结果是否溢出）
  • 这些标志信息通常会倍送入PSW程序状态寄存器中
  • PSW寄存器也称为“标志寄存器FR(Flag Register)”
  • Cin是进位输入信号、Cout是进位输出信号（类似于带标志位的加法器）

定点数的移位运算

算术移位

算术移位的对象是有符号数，在移位过程中符号位保持不变。

通过改变各个数码位和小数点的相对位置，从而改变各数码位的位权。

原码的算数移位

原码的算数移位：符号位保持不变，仅对数值位进行移位。

算数右移：

高位补0，低位超过小数点部分舍去。若当舍弃的位$\neq$0，则会丢失精度。

例：

$-20D$的用8位二进制表示形式为$1\ 0010100.$，最高位为符号位。

进行算数右移可得$1\ 0001010.$，十进制为-10D，右移一位相当于：$-20\div 2^1$

算数左移：

低位补0，高位舍弃。若舍弃的位$\neq$0，则会出现严重误差。

例：

$-20D$的用8位二进制表示形式为$1\ 0010100.$，最高位为符号位。

进行算数左移可得$1\ 0101000.$，十进制为-40D，右移一位相当于：$-20\times 2^1$。

若-80D用8位二进制表示$1\ 1010000$，最高位为符号位。

进行算数左移可得$1\ 0100000$，结果为-32D，出现严重误差。

反码的算数移位

正数的反码表示和原码表示相同，所以正数的移位规则和原码相同。

反码负数的数值位与原码相反，因此负数反码的移位运算规则下：

算数右移： 高位补1，低位舍弃。

高位补1，低位超过小数点部分舍去。若当舍弃的位=0，则会丢失精度。

算数左移： 低位补1，高位舍弃。

低位补1，高位舍弃。若舍弃的位=0，则会出现严重误差。

补码的算数移位

正数的补码表示和原码表示相同，所以正数的移位规则和原码相同。

负数补码=反码末位+1导致反码最右边几个连续的1都因进位而变0，直到进位碰到第一个0为止。

规律——负数补码中，最右边的1及其最右边同原码。最右边的1的左边同反码

算数右移（同反码）：高位补1，低位舍弃。

算数左移（同原码）：低位补0，高位舍弃。

总结可为如下图：

2-11

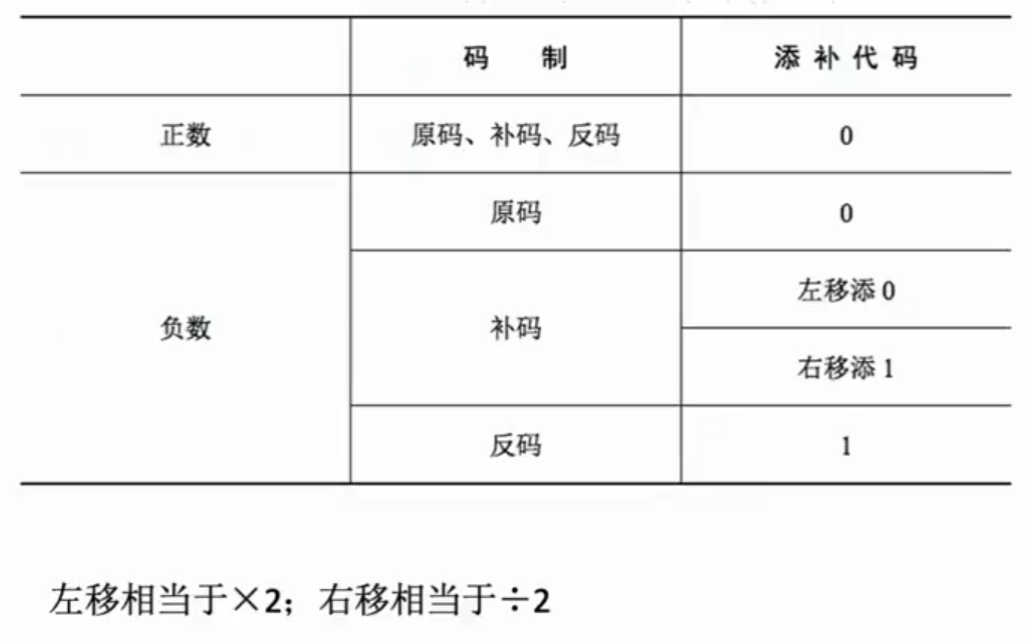
由于位数优先，因此有时候无法用算数移位精确的等效乘除法。

算数移位的应用举例：

若要实现$-20 \times 7$ ， 将7D转换为二进制$111B$，原式可变为$-20 \times(2^0+2^1+2^2)$。

即相当于 不左移+左移1位+左移两位 即可实现。
$$
-20\times 7 = 1\ 0010100+ 1\ 0101000+1\ 1010000=-160D
$$

逻辑移位

逻辑移位将操作数视为无符号数。

逻辑移位的规则很简单，逻辑右移时，高位补0，低位舍弃。逻辑左移时，低位补0，高位舍弃。

循环移位

循环移位是分带进位标志位CF的循环移位（大循环）和不带进位标志位的循环移位（小循环）。

循环移位的特点是，移出的数位又移入到数据中，而是否带进位则要看是否将进位标志位加入循环位移。

2-12

定点数的加减运算

在计算机内部中并没有小数点，只是人为约定了小数点的位置，小数点约定在最左边就是定点小数，小数点约定在最右边就是定点整数。因此在运算过程中只需关心符号位和数值位即可。

原码的加减运算

在原码加法中，若直接用加法器对其原码进行加法运算可能出错，如$14D=0001110$和$-14D=1001110$的二进制进行相加，结果为$10011100$，显然结果不正确。所以要用其他方法实现。

则可以归纳出原码的加法运算：

正+正 -> 绝对值做加法，结果为正（结果可能溢出）

负+负 -> 绝对值做加法，结果为负（结果可能溢出）

正+负 -> 绝对值大的减绝对值小的，符号同绝对值大的数

负+正 -> 绝对值大的减绝对值小的，符号同绝对值大的数

而原码的减法运算只需将“减数”的符号取反，即可转变为相应的加法运算。

补码的加减运算

由于原码想用电子器件实现过于复杂，所以计算机中一般适用补码来进行加减运算。

补码的加法运算：将符号位一同参与运算，即可得出相应的补码。

例：设机器字长为8位（含1位符号位），A=15，B=-24，则：
$$
[A+B]_补=0,0001111+1,11010000=1,1110111
$$
A+B的原码为10001001，真值为-9与十进制加法结果一致。

补码的减法运算只需把负号看成被减数的符号数即可转变为加法运算。

补码溢出判别方法

补码仅当在“正数+正数”才会上溢——正+正=负，“负数+负数”才会下溢——负+负=正

计算机来判断补码溢出方法有三种：

  1. 采用一位符号位

    设A的符号为$A_S$，B的符号为$B_S$，运算结果的符号为$S_S$，则溢出表达式为
    $$
    V=A_SB_S\overline{S_S}+\overline{A_S} \overline{B_S}S_S
    $$
    若V=0，表示无溢出；

    若V=1，表示有溢出。

  2. 采用一位符号位，根据数据位进位情况判断溢出符号位的进位$C_s$，最高数值位的进位$C_1$。

    当$C_s=0,C_1=1$时，就发生了上溢。

    当$C_s=1,C_1=0$时，就发生了下溢。

    即当$C_s$和$C_1$不同时就有溢出，此时逻辑表达式为$V=C_s⊕C_1$，若V=0，表示无溢出；V=1，表示有溢出。

  3. 采用双符号位

    正数符号为00，负数符号为11

    例：设机器字长8位（含1位符号位），A=15，B=-24，C=124

    $[A+C]_补=00,0001111+00,1111100=01,0001011$，结果真值-117

    $[B-C]_补=11,1101000+11,0000100=10,1101100$，结果真值+108

    记两个符号位为$S_{s1},S_{s2}$，则情况如下：

    1. $S_{s1}S_{s2}=00$：表示结果为正数，无溢出。
    2. $S_{s1}S_{s2}=01$：表示结果上溢，正溢出。
    3. $S_{s1}S_{s2}=10$：表示结果下溢，负溢出。
    4. $S_{s1}S_{s2}=11$：表示结果为负数，无溢出。

    溢出逻辑判断表达式为$V=S_{s1}⊕S_{s2}$，若V=0，表示无溢出；V=1，表示有溢出。

双符号位补码又称：模4补码（实际存储时只存储1个符号位，运算时会复制一个符号位），单符号位补码又称：模2补码

补码加减运算电路

2-13

根据图2-13，设这为4位加法器（最高位为符号位）被加数$X=0011B$，加数$Y=0100B$，此时加数为正，所以多路选择器的$Sub=0$，A和B会直接进行运算，最后加和结果为$0111B$会通过最上方的线直接输出。

若进行减法运算，此时多路选择器$Sub=1$，由于Cin和Sub相连，当$Sub=1$时，$Cin=1$，就实现了把原码变为补码的步骤。

无符号数的加减运算

无符号整数的加法：从最低位开始，按位相加，并往更高位进位。

由于n位寄存器自动实现$mod2^n$，假设要算$B-A$所以$A+A_反+1=2^n$，可以将A等价为$A_反+1$，然后$B-A=B+A_反+1$，必会产生高位进1，导致溢出，从而根据$mod2^n$，从而可将减法变为加法运算。

无符号整数的减法：

  1. “被减数”不变，“减数”全部位按位取反（可以获得减数的补数）、末位+1，减法变加法
  2. 从最低位开始，按位相加，并往更高位进位
无符号数加法/减法溢出判断

n bit无符号整数表示范围$0~2^n-1$，超出此范围则溢出。

计算机判断溢出方法：

  • 无符号加法的溢出判断：最高位产生进位=1时，发生溢出，否则未溢出。
  • 无符号减法的溢出判断：减法变加法，最高位产生的进位=0时，发生溢出，否则未溢出

定点数的乘除运算

原码的乘法运算

乘法运算可以通过累加和右移的操作来实现。

手算二进制乘法：手算二进制乘法和十进制的乘法如出一辙，根据十进制乘法相乘并错位相加即可。

例：

2-14

而拆分为2进制的运算，各位相乘并相加可得：
$$
0.1011=1\times 2^{-1} +0\times 2^{-2}+1\times 2^{-3}+1\times 2^{-4}\
0.1101=1101\times 2^{-4}(小数点左移四位)\
即:0.1101\times 0.1011 =(1101\times 1\times 2^{-8})+(1101\times 1 \times 2^{-7})+(1101\times 0 \times 2^{-6})+(1101\times 1\times 2^{-5})
$$

若考虑用机器实现则有以下几个问题需要思考：

  • 实际数字有正负，符号位如何处理？
  • 乘积的位数扩大一倍，如何处理？
  • 4个位积都要保存下来最后统一相加？

由上面的问题我们就可以引出定点数的乘法运算：

原码一位乘法

原码一位乘法的特点是符号位与数值位是分开计算，乘积符号由两个数的符号位“异或”形成，而乘积的数值部分则是两个数的绝对值相乘之积。

设$[x]_原=x_sx_1x_2\dots x_n,[y]_原=y_sy_1y_2\dots y_n$，运算规则如下：

  1. 被乘数 x 和乘数 y 均取绝对值参与yu你算，看作无符号数，符号位$x_s⊕y_s$。
  2. 部分积是乘法过程的中间结果。乘数每一位$y_i$乘以被乘数得$X\times y_i$后，将该结果与前面所得的结果累加，就是部分积，初值为0。
  3. 从乘数的最低为$y_n$开始判断：**若$y_n=1$，则部分积加上被乘数x，然后右移一位；若$y_n=0$**，则部分积加上0，然后右移一位。
  4. 重复步骤 3 ，判断n次。

例：

设机器字长位n+1=5（含一位符号位），$[x]_原=1.1101,[y]_原=0.1011$，采用原码一位乘法求xy。

符号位进行单独处理，此时**符号位=$x_s⊕y_s$**，而将x和y的数值位取绝对值，将被乘数x放入X（通用操作数寄存器）中，将乘数y放入MQ（乘商寄存器）中，并将ACC（累加器）清零，可得如下图2-15。

2-15

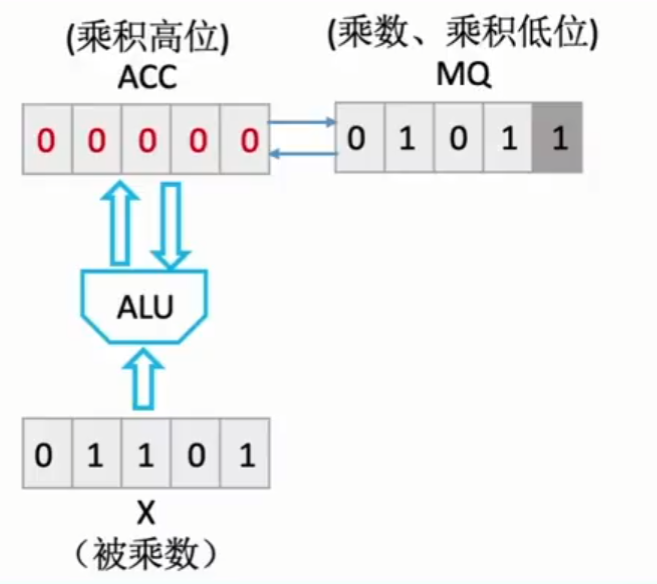
此时会先从01011（乘数）的最低位开始计算，若最低位=1，则ACC中会加上01101（被乘数），若最低位=0，则ACC加上0（即什么都不加）。

显然此时为1，因此ACC中会变乘01101，如下图所示。

2-16

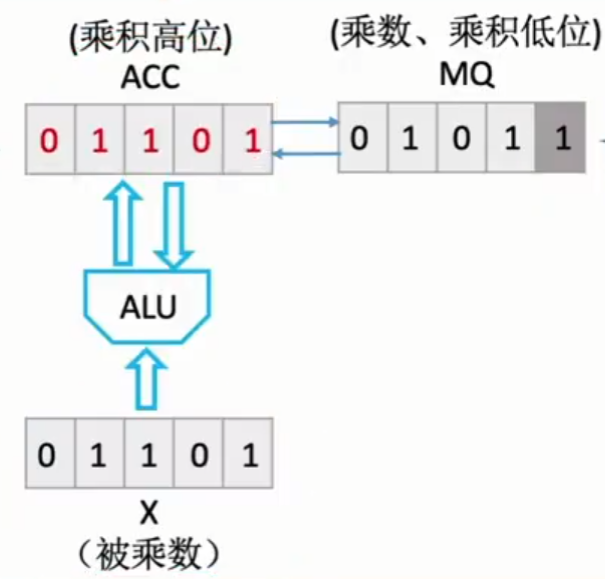
此时要算第二个位积，因为算第二个位积和第一位位积会产生一个错位，就可以通过ACC和MQ同时逻辑右移1位实现。高位补0，超过范围的最低位则直接丢弃，如下图。

2-17

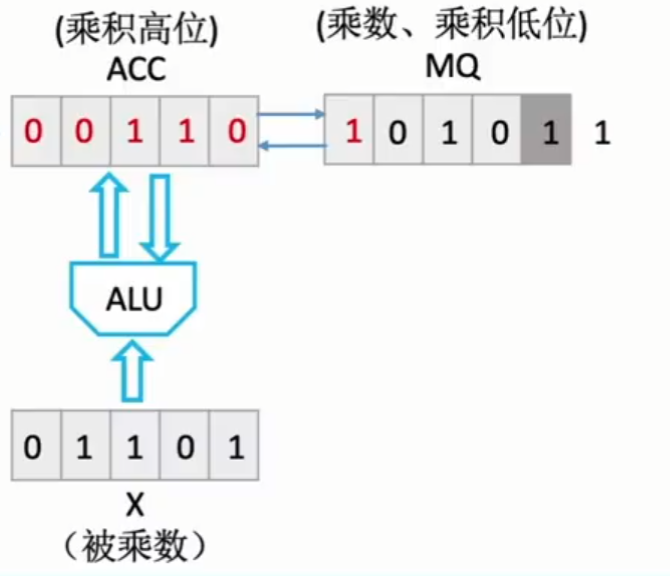
然后反复重复上方步骤，可得最终结果：

2-18

结果为$0.10001111$，与手算的结果一致，最后再加上符号位就为$-0.10001111$

补码的一位乘法（booth 算法）

设$[x]_补=x_sx_1x_2\dots x_n,[y]_补=y_sy_1y_2\dots y_n$，运算规则如下：

  1. 符号位参与运算，运算的数均以补码表示。
  2. 被乘数一般取双符号位参与运算，部分积取双符号位，初值为0，乘数取单符号位。
  3. 乘数末位增设附加位$y_{n+1}$，初值为0.
  4. 根据$(y_n,y_{n+1})$的取值来确定操作。
  5. 移位按补码右移规则进行。
  6. 按照上述规则进行n+1步操作，但第n+1步不再移位（进行n+1次累加和n次右移），仅根据$y_n$与$y_{n+1}$的比较结果做相应的运算。

可归纳为：

进行n轮加法、移位，最后再多来一次加法，每次**加法可能$+0、+[x]_补、+[-x]_补$ **，最终加什么是根据当前MQ中的最低位（乘数y的最低位）、辅助位来确定加什么。

  • 辅助位 - MQ中最低位 = 1 时， (ACC) + $[x]_补$
  • 辅助位 - MQ中最低位 = 0 时， (ACC) + 0
  • 辅助位 - MQ中最低位 = -1 时， (ACC) + $[-x]_补$

且每次右移的规则是补码的算数右移，并且符号位参与运算。

设机器字长为5位（含1位符号位，n=4），$x=-0.1101,y=+0.1011,[x]_补=1.0011,[y]_补=0.1011$，将x和y的补码放入运算器中，如下图：

2-19

由图可得除了MQ中均有双符号位参与运算。

2-20

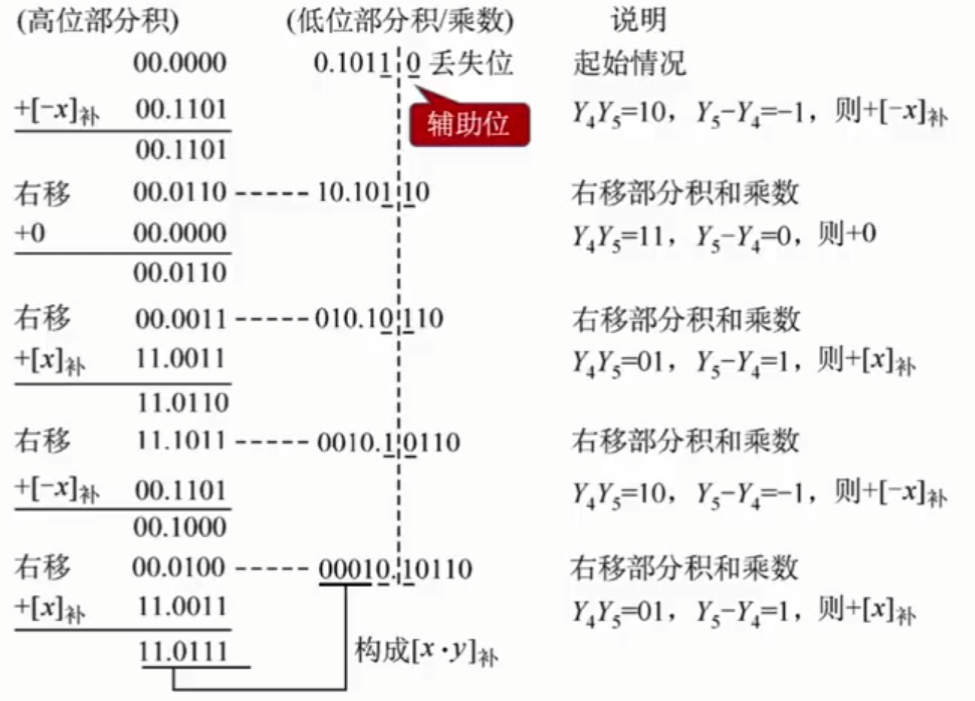
在图中加和值都会存到ACC中，然后ACC和MQ每次加完会统一进行算术右移。

原码的除法运算

符号拓展

在算数运算中，有时必须把带符号的定点数转换成具有不同位数的表示形式。例如，某个程序要将8位整数与32位整数相加，要想得到正确的结果，在8位和32位整数相加之前，必须将8位转换成32位整数形式，这称为“符号拓展”。

正数的符号扩展

正数的符号扩展非常简单，即符号位不变，新表示形式的所有扩展位都用0进行填充。

负数的符号扩展

原码表示的负数的符号拓展与正数相同，只不过此时符号位为1。

补码表示负数的符号拓展方法：新表示的所有附加位都用1（对于正数）或0（对于小数）进行补充。

手算除法（二进制）

设机器字长为5位（含1位符号位，n=4），$x=0.1011,y=0.1101$求x/y。

模仿十进制除法规则，可得二进制除法：

2-21

最后算出的余数由于先前右移了4位所以要再左移4位，即为$0.00000111$，结果就为$x/y=0.1101$，余数$0.00000111$

恢复余数法

对于原码的正负性会单独用异或运算来进行处理，即$x_s⊕y_s$，数值位取绝对值进行除法计算。

设机器字长为5位（含1位符号位，n=4），$x=0.1011,y=0.1101$求x/y。

此时$|x|=0.1011,|y|=0.1101,[|y|]_补=0.1101,[-|y|]_补=1.0011$，将x，y放入运算器中：

2-22

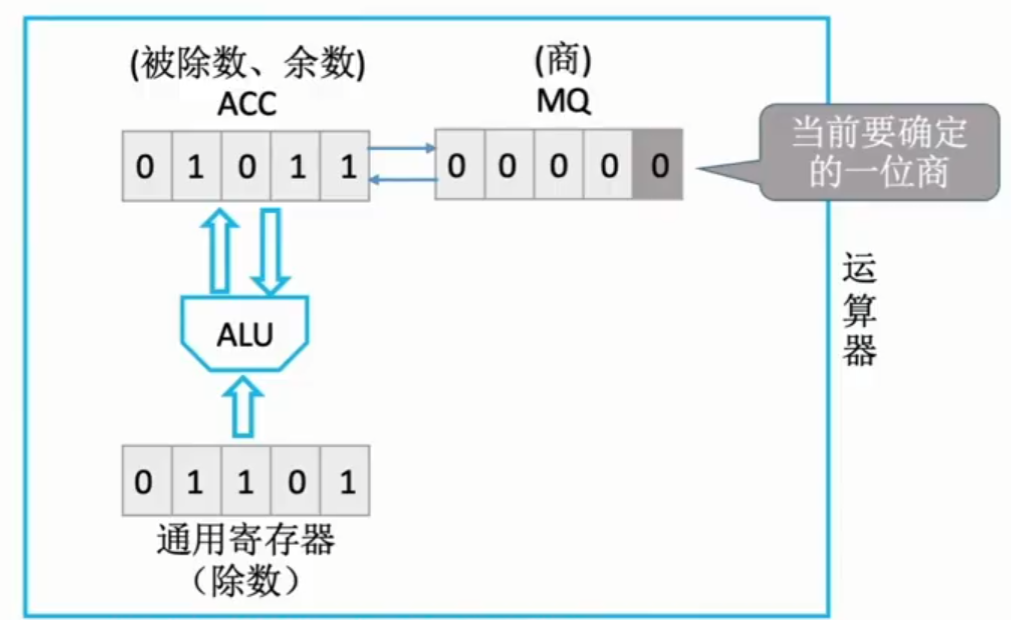
由于计算机并不直到除数和被除数谁更大，所以规定默认先上商1，如果搞错了再改上商0，并“恢复余数”（恢复余数通过加上除数y来进行恢复）

2-23

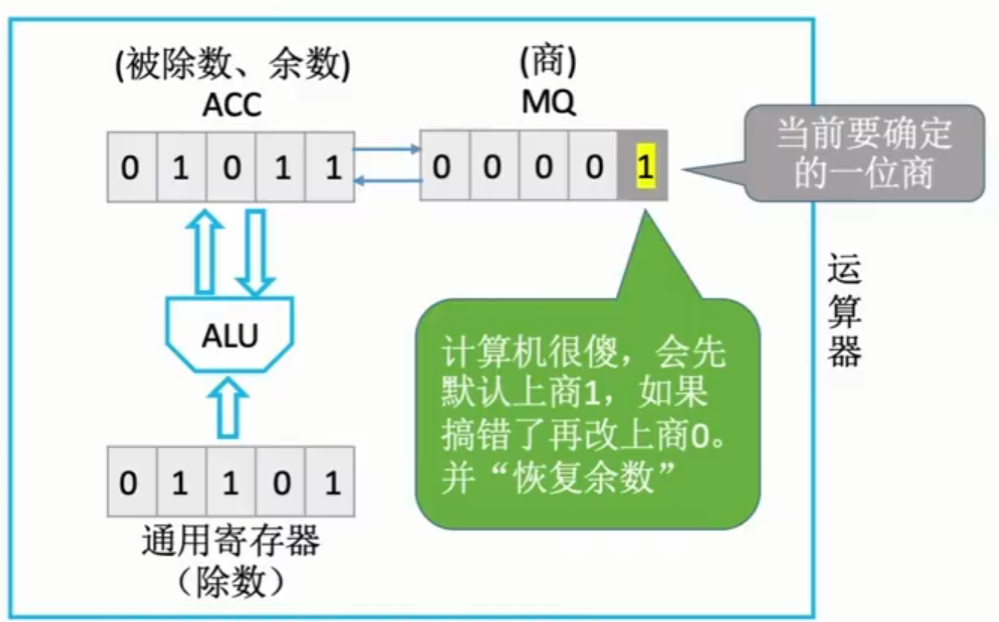
第一次运算 ACC-除数（通用寄存器）-> $|x|+[-|y|]_补=01011+10011=11110$，此时计算结果为负数，说明上商1为错误，所以需要恢复余数再重新该上商0.

2-24

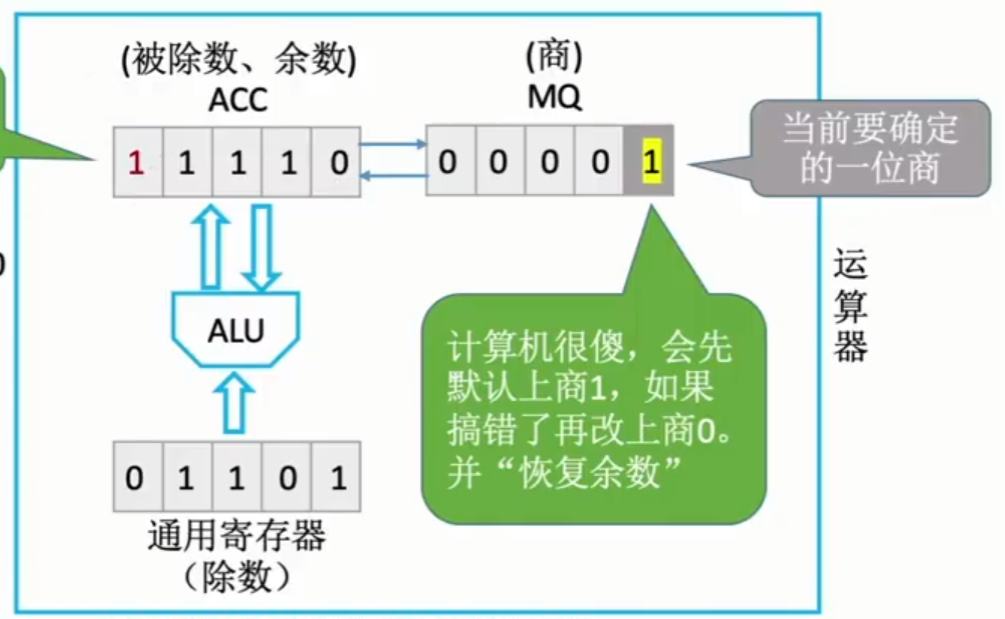
此时图2-24就为商错，需要恢复余数后再重新商0.

2-25

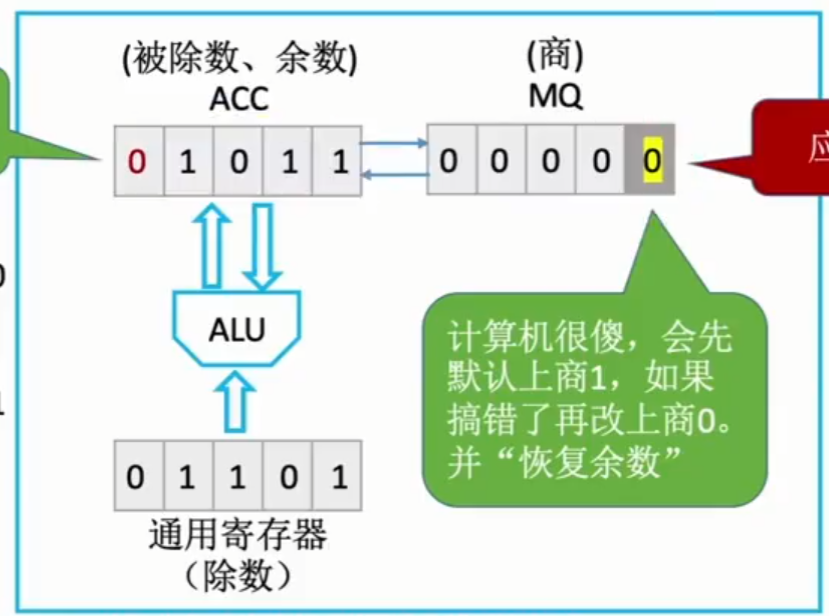
由于余进行下一步运算要错位，所以ACC可以通过逻辑左移实现错位的功能，即将MQ的最高位移至ACC的最低位。

2-26

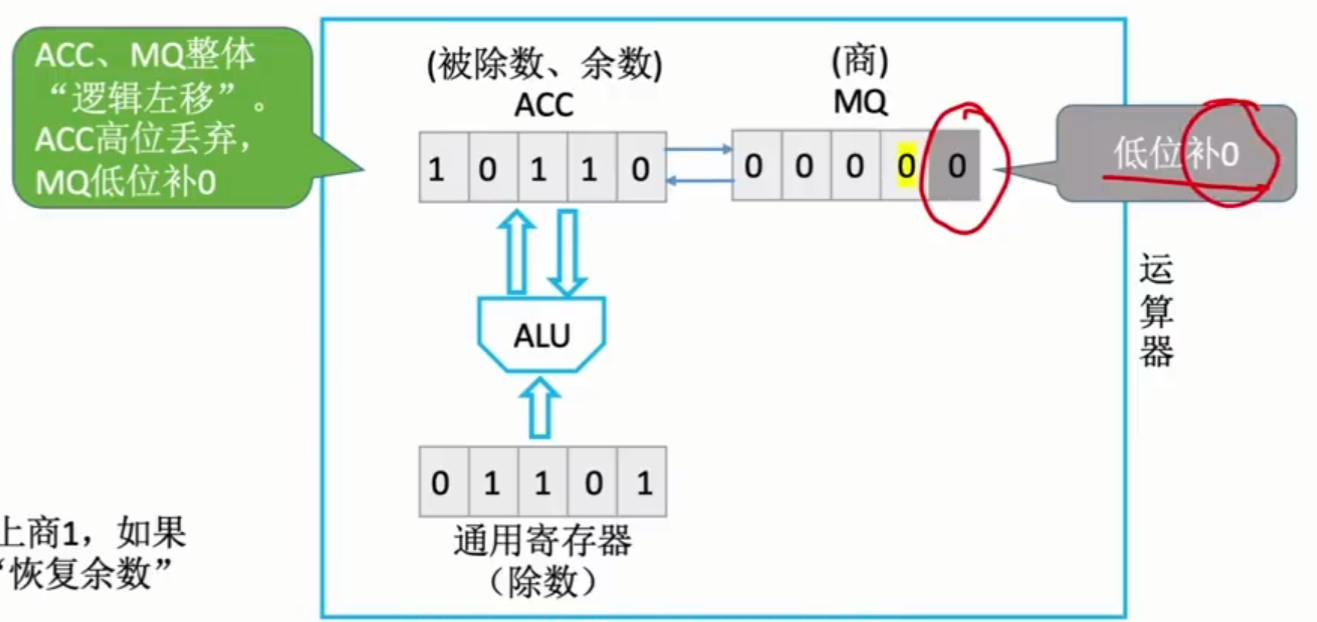
进行下一次运算计算机还是会默认商1，若商错再恢复余数商0，如此循环可得到最终结果和余数：

2-27

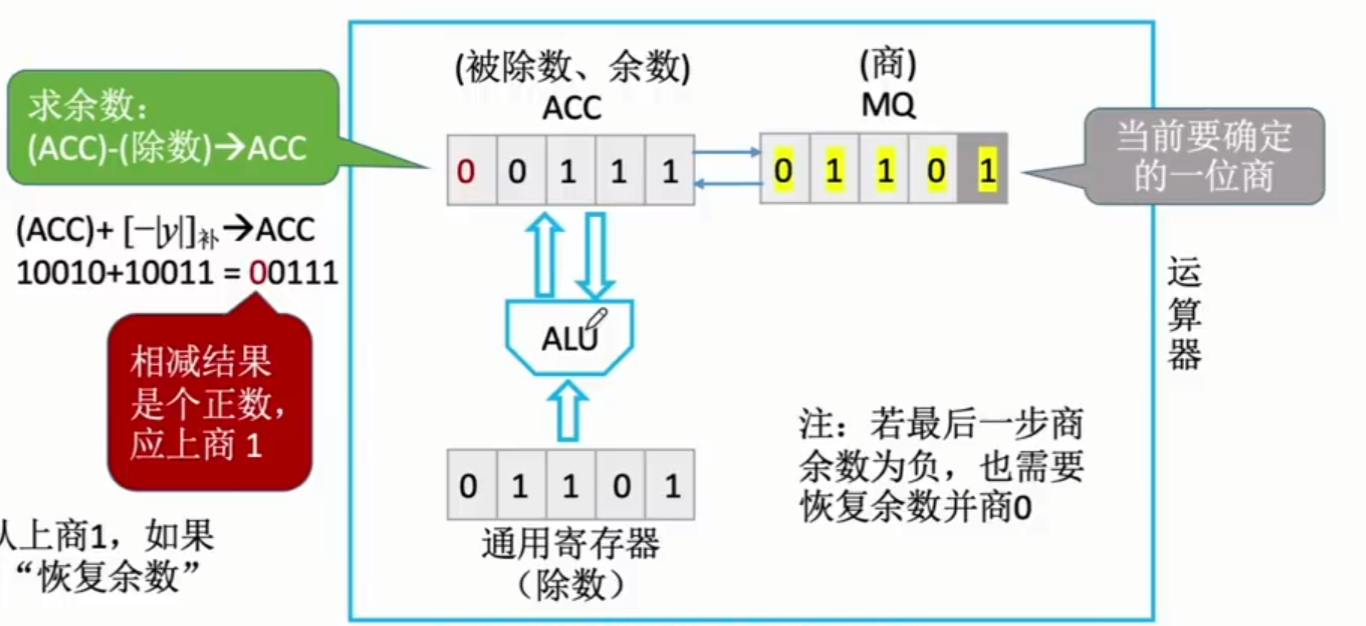
此时MQ中就存放着商的结果，ACC中则存放着余数，与手算结果一致。

手算实现恢复余数法

2-28

模仿计算机每次都先商1，若商错则通过$+[|y|]_补$恢复余数后再商0，如此往复可得到最终结果。

加减交替法

在恢复余数法的基础上，若商1为负时，可以通过直接将余左移一位，加上$[|y|]_补$可以直接实现得到恢复余数后的结果。符号位同样通过异或单独确定，即$x_s⊕y_s$。

2-29

注：当最后一步余数为负时，需要商0，再加上$[|y|]_补$后才能获得正确余数

补码的除法运算

补码的除法运算主要以加减交替法为主，因此和原码的加减交替法会有很多相似的地方。

补码除法的特点是：

  • 符号位与数值位一起参加运算，商符自然形成。补码的被除数、余数、除数回采用双符号位。
  • 若被除数与除数同号，商1，余数左移一位减去除数
  • 若被除数与除数异号，商0，余数左移一位加上除数

例：

设机器字长为5位（含1位符号位，n=4），$x=+0.1000,y=-0.1011$，采用补码加减交替法求x/y，$[x]_补=00.1000,[y]_补=11.0101,[-y]_补=00.1011$。

2-30

注：若对商的精度没有特殊要求，则一般采用“末位商恒置1”

C语言中整数类型及类型转换

注：C语言中定点整数都是用“补码”的形式进行存储

C语言中用unsigned关键字来修饰就代表是无符号类型。

先观察以下代码：

void main(){
    short x = -4321;		//short型占用2个字节
    unsigned short y = (unsigned short)x; //赋值会带符号位一起赋值给y。
    
    int a = 165537, b = -34991;		//int型占用4个字节
    short c = (short)a, d = (short)b;	//short型占用2个字节  将长整数变短整数会高位截断，保留低位。
    
    short x = -4321;
    int m = x;  //将短整形转长整形是直接符号拓展，若符号位1则全补1，符号位为0则全补0
    unsigned short n = (unsigned short) x;
    unsigned int p = n;
}

数据的存储和排列

数据的“大小端模式”

在存储数据时，数据从低位到高位可以按从左往右排列，也可以按从右往左排列。因此，无法用最左和最右来表示数据的最高位和最低为，通常用最低有效字节（LSB）和最高有效字节（MSB）来表示数的低位和高位。例如，在32位计算机中，一个int型变量 i 的机器数位 01 23 45 67H，其最高有效字节MSB = 01H， 最低有效字节 LSB = 67H。

多字节数据都存放在连续的字节序列中，根据数据中各字节在连续字节序列中的排列顺序不同，可以采用两种排列方式： 大端方式（big endian）、小端方式（little endian）。

假设存4字节int: 01 23 45 67 H，

2-31

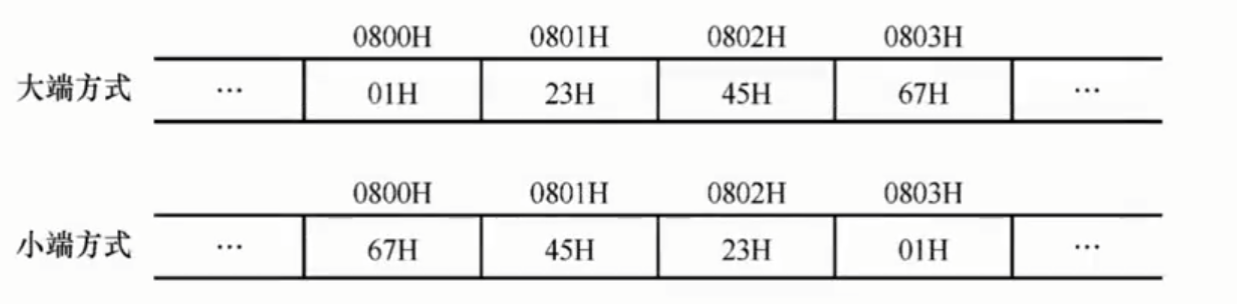
大端模式是按从最高有效字节到最低有效字节的顺序存储数据，即最高有效字节放在前面；

小端方式是按从最低有效字节到最高有效字节的顺序存储数据，即最低有效字节放在前面；

边界对齐

现代计算机通常按字节编址，即每个字节对应1个地址

通常也支持按字、按半字和字寻址。假设存储字长为32位，则1个字 = 32bit，半字 = 16 bit。每次访存只能读/写1个字。

2-32

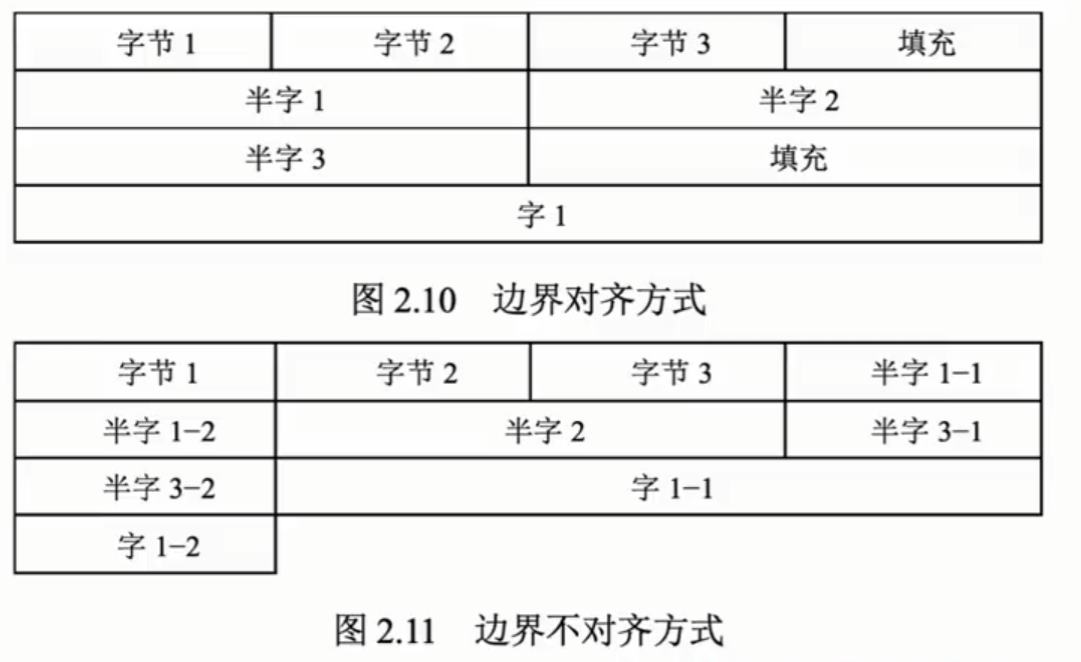
边界对齐就是用空间换时间的一种存储方式

文章作者: LsWorld
文章链接: http://example.com/2023/11/21/ji-suan-ji-zu-cheng-yuan-li-shu-ju-de-biao-shi-yu-yun-suan/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 LsWorld !
计算机组成原理 数制与编码
评论
  目录