电路的等效变换
在了解电路的等效变换前先了解什么是电阻电路。
电阻电路就是仅由电源和线性电阻构成的电路。
分析方法:
- 欧姆定律和基尔霍夫定律来分析。
- 等效变换的方法,也称化简。
电路的等效变换基于两端电路:两端电路即任何一个复杂的电路, 向外引出两个端钮,且从一个端子流入的电流等于从另一端子流出的电流,则称这一电路为二端网络 (或一端口网络),如1-1所示。
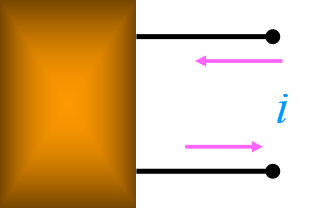
两端电路等效的概念
两个两端电路,端口具有相同的电压、电流关系,则称它们是等效的电路,即对于两个两端电路,他们电压和电流大小相同,参考方向也相同,即可将两个电路互相进行交换,并对外等效,如1-2图所示。

电路等效变换的条件
两电路具有相同的VCR,即电压电流电阻值相同即可等效变换。
电阻的串联与并联
电阻的串联
电阻串联的性质:
- 电流相等,流过同一电流。
- 总电压等于各串联电阻的电压之和。
- 串联总电阻为电阻值相加。
- 电压之比等于电阻之比(串联分压)。
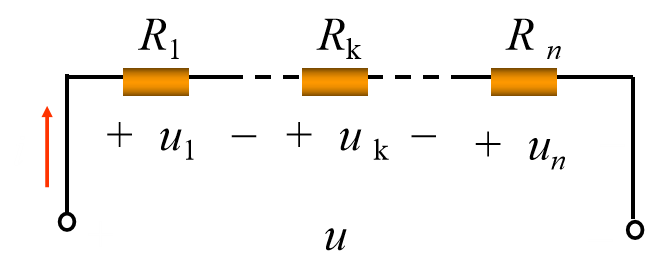
电阻的并联
电阻并联的性质:
- 并联电路电压相等。
- 总电流等于各串联电阻的电流之和。
- 电流之比等于电阻的反比比(并联分流)。

并联求总电阻公式:
$$
R_总 = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \dots + \frac{1}{R_n}}
$$
电阻的Y形连接和∆形连接的等效变换
Y形和∆形如图3-1和图3-2所示。
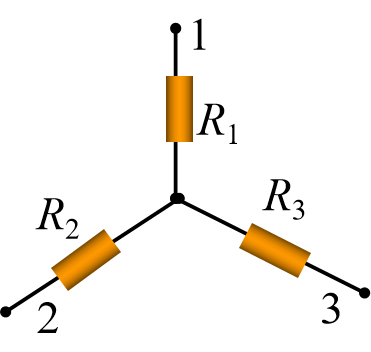

电阻的Y三角转换:
从三角形变成Y形
由图3-2转图3-1,电阻的等效变换可以变成对外等效,所以可以获得对外等效电阻的公式:
$$
R_1 = \frac{R_{12}R_{31}}{R_{12}+R_{23}+R_{31}}\
R_2 = \frac{R_{12}R_{23}}{R_{12}+R_{23}+R_{31}}\
R_3 = \frac{R_{23}R_{31}}{R_{12}+R_{23}+R_{31}}\
$$
Y形变成三角形
由图3-1转图3-2,电阻的等效变换可以变成对外等效,所以可以获得对外等效电阻的公式:
$$
R_{12} = \frac{R_{1}R_{2}+R_2R_3+R_3R_1}{R_3}\
R_{23} = \frac{R_{1}R_{2}+R_2R_3+R_3R_1}{R_1}\
R_{31} = \frac{R_{1}R_{2}+R_2R_3+R_3R_1}{R_2}\
$$
电压源、电流源的串联和并联
理想电压源
串联情况

图4-1为n个电压源的串联(参考方向相同,若有些参考方向相反则前面为负号),可以用一个电压源等效替代,且这个等效电压源激励电压为:
$$
u_s = u_{s1} + u_{s2} + \dots + u_{sn} = \sum_{k=1}^{n}{u_{sk}}
$$
理想电压源等效的电压源之值等于所有电压源的代数和。
并联情况(仅当每个电压源电压相同)
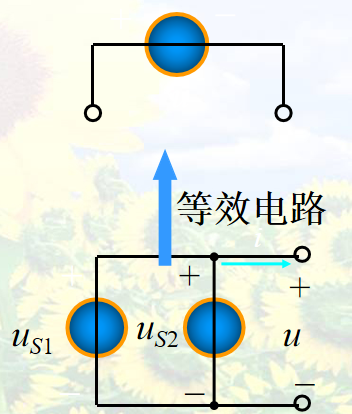
理想电流源
并联情况
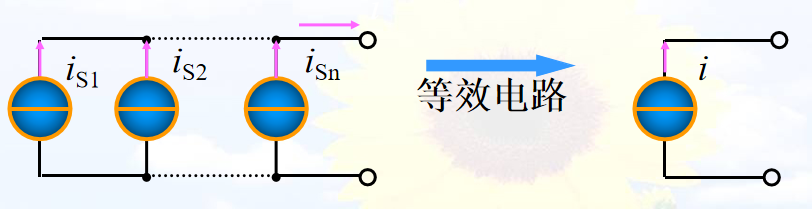
图4-2为n个电压源的并联(参考方向相同,若有些参考方向相反则前面为负号),可以用一个电压源等效替代,且这个等效电压源电流为:
$$
i_s = i_{s1} + i_{s2} + \dots + i_{sn} = \sum_{k=1}^ni_{sk}
$$
理想电流源等效的电流源之值等于所有电流源的代数和。
串联情况
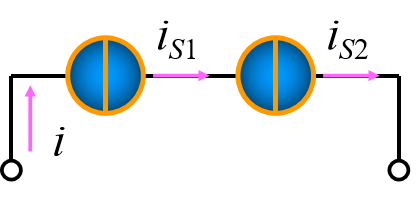
串联情况下电流处处相等,所以可以等效为电流为i的电流源。
实际电压源与电流源间的相互转换
仅当电压源和电流源及电阻满足以下条件可进行相互转换:
- 两种实际电源的内阻相同,及下图4-4中$$R_S=G_S$$
- 电压源U与电流源I满足条件:$$U_S=I_SR_S$$(电压源电压等于电流源电流及电流源的电阻)。
- 两种电源模型流出电流的方向相同。
电压源变换为电流源

转换公式为:
$$
i_S = \frac{u_S}{R_S} \quad G_S = R_S
$$
电流源变换为电压源

转换公式为:
$$
u_S =i_SG_S \quad R_S = G_S
$$
无论电流源转电压源还是电压源转电流源,转换过后电压或电流方向都与原先的相反,流出的方向相同!

