数电-数字逻辑概论

数制

数制的概念就不过多赘述，这里主要描述十进制，二进制，八进制以及十六机制间的相互转换。

十-二-八-十六进制之间的转换

二进制转十进制

按位权进行展开再求和。

例：
$$
(101110.011)2 = 1 \times 2^5 + 0 \times 2^4 + 1 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 + 0\times 2^{-1} + 1 \times 2^{-2} + 1 \times 2^{-3} = (46.375){10}
$$

十进制转二进制

十进制通过除2即可将再将每次除过后的余数保存下来并倒序即可获得相应的二进制数。整数部分采用“除基取余，小鼠部分采用“乘基取整法”

例：$$(26.375)_{10}$$

整数部分（%代表取余）：26%2 = 0 ，后再将 13 % 2 = 1 （13是通过26/2算出），后 6 % 2 = 0，再 3 % 2 = 1，最后 1%2 = 1，一直除到商为0为止。将取到的余倒序，则得整数二进制$$(11010)_2$$。

小数部分：$$0.375\times 2 = 0.750$$整数部分为0，后$$0.750 \times 2 = 1.500$$整数部分为1，取出，后$$0.500 \times 2 = 1.000$$整数部分为1取出。最后小数部分顺序得小数二进制$$(.011)_2$$。

合在一起得：$$(26.375)_{10} = (11010.011)_2$$

十进制转八进制或十六进制就是将除部分改为8或16。

二进制与八、十六进制相互转换

二进制转八进制与十六进制：

从小数点开始，整数部分向左、小数部分向右三位一组（十六进制以四位一组），不足三位（四位）的加0补足，再按顺序写出各组对应的八进制数（十六进制数）。

以八进制为例：

$$(11\quad 100\quad 101.\quad111\quad 010\quad 11)_2$$，整数部分以三位一组，得$$011\quad 100\quad 101$$（补了一位0）后将每三位换成八进制得$$(345)_8$$，小数部分则右补零得$$.111\quad 010\quad 110$$（补了一位0），后转为八进制$$(.726)_8$$，最后结果就位$$(345.726)_8$$，十六进制也是同理。

八进制与十六进制转二进制：

每位八进制数（十六进制数）用三位二进制（四位二进制）数来代替，再按原顺序排列。

以八进制为例：

$$(745.361)_8$$，将整数小数部分分为三位一组二进制即可得$$(111\quad 100\quad 101.\quad011\quad 110\quad 001)$$

码制

码制就是一系列编码的格式，而将若干个二进制数码0和1按一定规则排列来表示某种特定含义的代码就是二进制代码。用数码的特定组合来表示特定信息的过程就称编码。常见的二进制代码有：自然（态序）二进制码，二-十进制码（BCD码）、格雷码、奇偶校验码、ASCII码

二-十进制码

又称BCD码，就是用四位二进制数来表示十进制数中的0-9十个数码。

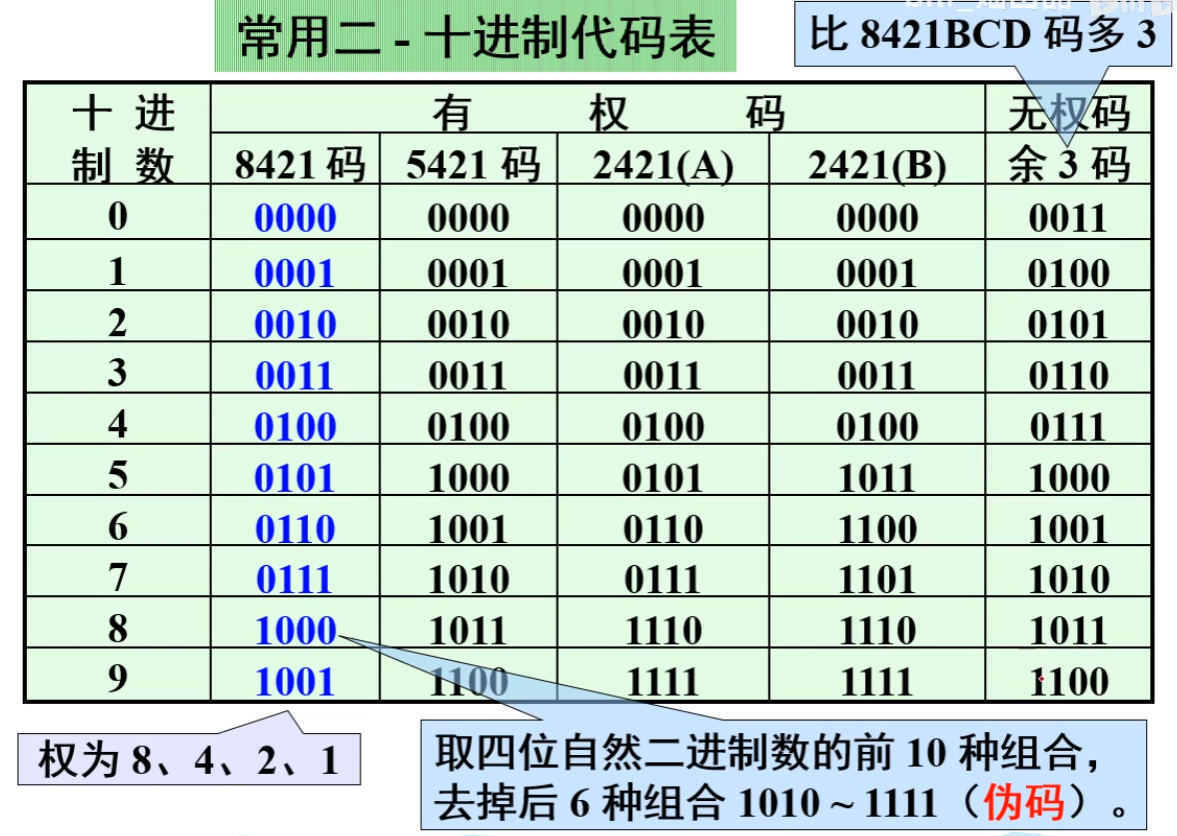
图1-1就是各种常见的BCD码。

例：用BCD码表示十进制数举例（用BCD码，每位十进制数用四位二进制来表示）：

$$(36){10}=(0011\quad 0110){8421BCD}$$

$$(4.79){10}=(0100\quad.0111\quad 1001){8421BCD}$$

$$(0101.0001){8421BCD}=(5.1){10}$$

BCD码与数制的区别：

$$(150){10}=(0001\quad 0101 \quad 0000){8421BCD} = (10010110)_2=(226)8=(96){16}$$

基本逻辑运算和复合逻辑运算

与或非运算

与或运算与计算机语言中&&、||意思相同。

与运算中，表达式A和B都为真（即都为1）时候才为真，或运算中，表达式A和B其中有一个为真（即其中一个为1）时候为真。例A=1 && B=1则为true，A=1 || B = 0为true，而A=1 && B = 0为false

与运算逻辑表达式： $$Y=A· B$$或$$Y=AB$$

逻辑符号：

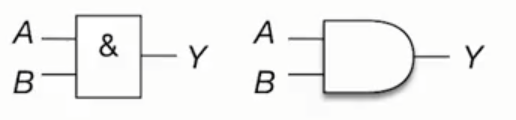
或运算逻辑表达式： $$Y=A+B$$

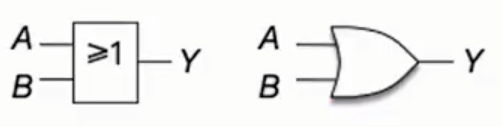
非运算表达式：$$Y=\bar{A}$$，即$$\bar{0}=1 \quad \bar{1}=0$$

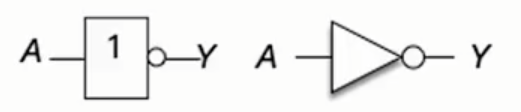
复合逻辑运算

与非运算（NAND）

与非运算表达式：$$Y=\overline{AB}$$，即有0出1，全1出0；

或非运算（NOR）

或非运算表达式：$$Y=\overline{A+B}$$，即有1出0，全0出1；

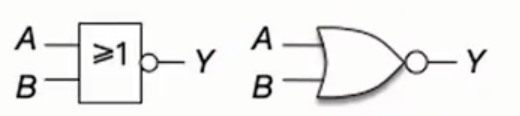
异或运算（Exclusive-OR）

异或运算表达式：$$Y=A⊕B=\bar{A}B+A\bar{B}$$，即相同为0，不同为1；

若有奇数个1，则异或结果为1；若有偶数个1，则异或结果为0.

例：
$$
1⊕0⊕0⊕1⊕1⊕0⊕1=0\
1⊕0⊕1⊕0⊕1⊕1⊕1=1
$$

同或运算（Exclusive-NOR，即异或的非）

同或运算表达式：$$Y=A⊙B$$，即相同为1，不同为0；

若有奇数个1，则同或结果为0；若有偶数个1，则同或结果为1.

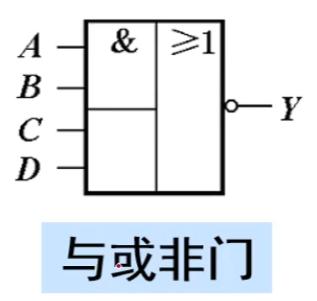
与或非运算（AND-OR-INVERT）

与或非运算表达式：$$Y=\overline{AB+CD}$$，先与后或再非；

逻辑代数的基本定律

常量间的计算

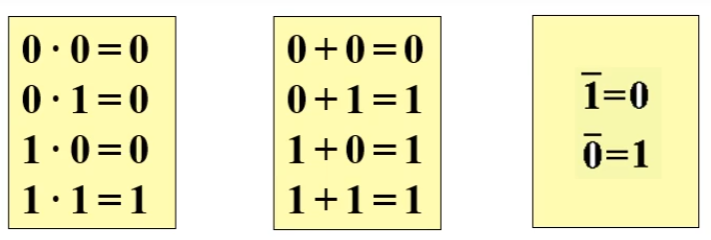
逻辑变量与常量的计算

0-1律

$$
0+A=A\
1+A=1\
0 \cdot A=0\
1 \cdot A = A
$$

同一律

$$
A+A=A\
A\cdot A = A
$$

互补律

$$
A+\bar{A} = 1\
A \cdot \bar{A} = 0
$$

还原律

$$
\bar{\bar{A}} = A
$$

逻辑代数的基本定律

交换律

$$
A+B=B+A\quad A\cdot B= B \cdot A
$$

结合律

$$
(A+C)+C = A+(B+C)\quad (A\cdot B)\cdot C= A \cdot (B\cdot C)
$$

分配律

$$
A(B+C) = AB+AC \quad A+BC=(A+B)(A+C)
$$

摩根定律（反演律）

$$
\overline{A\cdot B} = \bar{A} + \bar{B} \quad \overline{A+ B} = \bar{A} \cdot \bar{B}
$$

证明等式$$A+BC=(A+B)(A+C)$$：
$$
(A+B)(A+C)=AA+AC+AB+BC=A(1+C)+AB+BC\quad 注：1+C=1\
=A+AB+BC\
=A(1+B)+BC=A+BC
$$
证毕。

逻辑代数的常用公式

$$
AB+A\bar{B} = A \qquad A+AB=A\
A+\bar{A}B = A + B
$$

冗余律

$$
AB+\bar{A}C+BC = AB+\bar{A}C\
\overline{AB+\bar{A}C} = A\bar{B}+\bar{A}\bar{C}
$$

关于异或运算的一些公式

$$A⊕B=\bar{A}B+A\bar{B}$$
$$
A⊕B=B⊕A\
(A⊕B)⊕C=A⊕(B⊕C)\
A\cdot (B⊕C)=AB⊕AC\
A⊕1=\bar{A}\
A⊕0=A\
A⊕A=0\
A⊕\bar{A}=1\
$$
如果$$A⊕B=C$$则有$$\begin{cases} A⊕C=B\ B⊕C=A \end{cases} $$

逻辑代数的基本规则

代入规则

将逻辑等式两边的某一变量均用同一个逻辑函数替代，等式仍然成立。

例：$$A+\bar{A}B=A+B$$

$$A$$均用$$\bar{A}$$代替得：$$\bar{A}+AB=\bar{A}+B$$等式仍然成立。

反演规则

对任一逻辑函数式Y，将式子中的所有的”$$\cdot$$“换成“+”，“+”换成”$$\cdot$$“，“0”换成“1”，“1”换成“0”，原变量换成反变量，则得到原逻辑函数的反函数$$\bar{Y}$$，并不改变运算顺序。

例：$$Y_1=A(B+C)+CD$$，取反得：$$\bar{Y_1}=(\bar{A}+\bar{B}\bar{C})(\bar{C}+\bar{D})$$

对偶规则

对任一逻辑函数式Y，将式子中的所有的”$$\cdot$$“换成“+”，“+”换成”$$\cdot$$“，“0”换成“1”，“1”换成“0”，，则得到原逻辑函数的对偶式$$Y’$$。

逻辑表达式

表示输出函数和输入变量逻辑关系的表达式称逻辑表达式，逻辑表达式一般根据真值表、卡诺图或逻辑图写出。

常见表达式

$$Y=A\bar{B}+BC$$（与—或表达式）。

$$Y=(A+B)(\bar{B}+C)$$（或—与表达式）。

$$Y=\overline{\overline{A\bar{B}}\overline{BC}}$$（与非—与非表达式）。

$$Y=\overline{\overline{A+B}+\overline{\overline{B}+C}}$$（或非—或非表达式）。

最小项

在逻辑函数中，如果一个与项包含该逻辑函数的全部变量，且每个变量只出现一次，则称与项的最小项。对于n个变量的逻辑函数共有$$2^n$$个最小项。

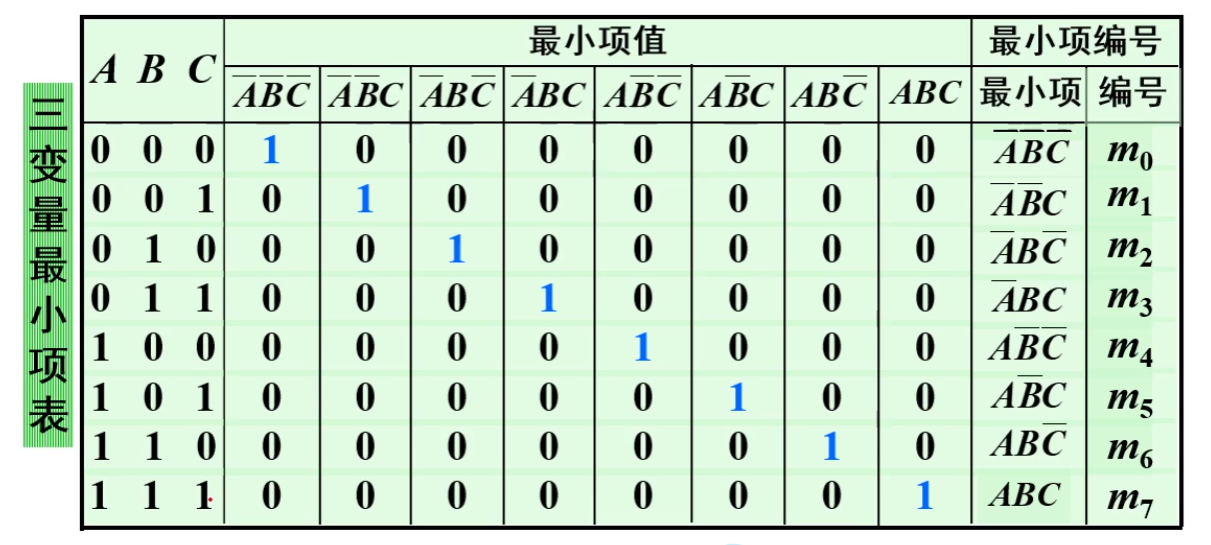
最小项的基本性质

1. 对于变量的任一组取值，只有一个最小项的值为1。
2. 不同的最小项，使其值为1的那组变量取值也不同。
3. 对于变量的同一组取值，任意两个最小项与的结果为0.
4. 对于变量的同一组取值，全部最小项逻辑或的结果为1.

最小项编号

最小项用$$m_i$$表示，通常用十进制数作最小项的下标。

编号方法是：将最小项中的原变量当作1，反变量当作0，从而得二进制，再将二进制转为对应的十进制数即为最小项的编号。

例：

$$\overline{A}BC$$的二进制$${011}_2$$，转为十进制为3，则下标就为3，最小项就是$$m_3$$

最小项表达式（标准与或表达式）

任何逻辑函数都是由其变量的若干个最小项构成，都可以表示成为最小项之和的形式。

在与或表达式中，有时与项并不是最小项，可利用$$\overline{A}+A=1$$的形式补充缺少的变量，将逻辑函数变成最小项之和的形式。

例：

$$Y=F(A,B,C)=AB+\overline{A}C$$，进行增项

使$$AB+\overline{A}C=AB(\overline{C}+C)+\overline{A}C(\overline{B}+B)$$，最后展开即可得最小项：

$$AB\overline{C}+ABC+\overline{A}C\overline{B}+\overline{A}CB$$

逻辑函数的化简

不同形式逻辑式由不同的最简式，一般先求取最简与或式，然后通过变换得到所需最简式。

最简与或式

1. 乘积项（即与项）的个数最少，使与门个数最少。
2. 每个乘积项中的变量数最少，使与门输入端数最少，

最简与非-与非式

1. 非号个数最少，使与非门个数最少。
2. 每个非号中的变量数最少，使与非门的输入端数最少。

公式化简法

并项法

运用$$AB+A\overline{B}=A(B+\overline{B})=A$$，将两项合并为一项，并消去一个变量。

吸收法

运用$$A+AB=A(1+B)=A$$和$$AB+\overline{AC}+BC=AB+\overline{AC}$$，消去多余的与项。

消去法

运用$$A+\overline{A}B=A+C$$or $$\overline{A}+AB = \overline{A}+B$$，消去多余因子。

配项法

在函数某一项乘$$A+\overline{A}=1$$，将一项展开两项，或用$$AB+\overline{A}C=AB+\overline{A}C+BC$$，增加冗余项。